Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: 2da Oportunidad - 1er Cuatrimestre 2007
Día: 25/05/2007
Enunciado
- Analizar si existen valores reales de
 y
y  para los cuales la curva parametrizada por:
para los cuales la curva parametrizada por: 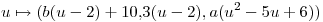 es perpendicular en el punto
es perpendicular en el punto 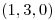 a la superficie de ecuación:
a la superficie de ecuación: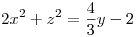 .
. - Sea
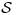 la superficie parametrizada por:
la superficie parametrizada por: 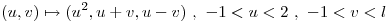 . Hallar un vector tangente en
. Hallar un vector tangente en 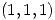 a la intersección de
a la intersección de 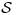 con el plano de ecuación
con el plano de ecuación 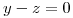 .
. - Sea
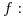 una función
una función 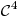 y sea
y sea 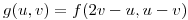 . Hallar si existen valores reales
. Hallar si existen valores reales  y
y  para que la función
para que la función 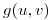 tenga extremo en el punto
tenga extremo en el punto  , sabiendo que el polinomio de Taylor de la función
, sabiendo que el polinomio de Taylor de la función  de grado 3 en
de grado 3 en 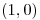 es
es 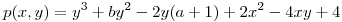 .
. - La función de producción de una empresa es:
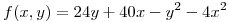 . El costo para la compañía es de $16 por unidad de
. El costo para la compañía es de $16 por unidad de  y de $8 por unidad de
y de $8 por unidad de  . Si la empresa desea que el costo total de los insumos sea de $176 calcule la máxima producción posible dada esa restricción en el presupuesto.
. Si la empresa desea que el costo total de los insumos sea de $176 calcule la máxima producción posible dada esa restricción en el presupuesto. - Demostrar que es posible definir de manera implícita
 y
y  de:
de: 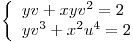 como función de
como función de  e
e  de manera única cerca del punto
de manera única cerca del punto  . Hallar
. Hallar 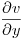 en el punto
en el punto  .
.
Resolución
Punto I
Para que la curva sea ortogonal a la superficie en el punto 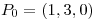 deber cumplirse que, el verctor director de la recta tangente a la curva, evaluada en dicho punto, sea paralela a la normal de la superficie en cuestión.
deber cumplirse que, el verctor director de la recta tangente a la curva, evaluada en dicho punto, sea paralela a la normal de la superficie en cuestión.
En primer lugar se evalua si existen valores para los cuales la curva pasa por el punto 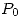 .
.
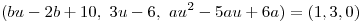
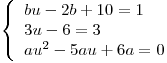
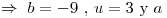 sin condiciones.
sin condiciones.
Luego se deriva la curva parametrizada para sacar el vector tangente:
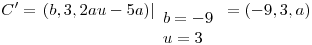
Se calcula la normal a la superficie 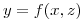
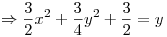
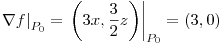
Por lo tanto, la normal a la superficie en  es
es 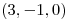 .
.
Finalmente resta comprobar que la normal y el vector tangente sean paralelos:
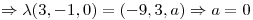
Resultado: 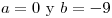
Punto II
La resolusíon de este problema consiste, básicamente, en hallar las normales en 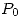 de la superficie y el plano en cuestión; su producto vectorial es justamente el la recta pretendida.
de la superficie y el plano en cuestión; su producto vectorial es justamente el la recta pretendida.
En primer lugar se evalua si existen valores para los cuales la superficie pasa por el punto 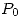 .
.
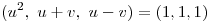
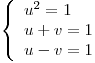
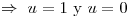 .
.
Luego se deriva la superficie parametrizada respecto de cada una de las variables y posteriormente se realiza el producto vectorial para obtener la normal a la superficie:
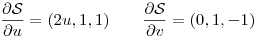
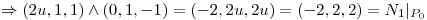
La normal del plano 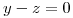 es
es 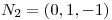 .
.
Por último se calcula el producto vectorial entre 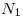 y
y  :
:
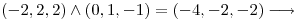 vector tangente.
vector tangente.
