Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: 2da Oportunidad - 2do Cuatrimestre 2007
Día: 24/11/2007
Enunciado
1) Sea 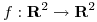 y su polinomio de Taylor de orden 2 en
y su polinomio de Taylor de orden 2 en 
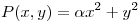
a) Demostrar que la gráfica de  es tangente al plano
es tangente al plano  en
en 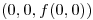 .
.
b) Demostrar que si 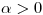 entonces
entonces  tiene un mínimo en
tiene un mínimo en  .
.
c) Demostrar que si 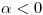 entonces
entonces  tiene un punto silla en
tiene un punto silla en  .
.
2) Sea el sistema
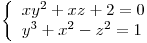
en un entorno de 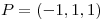 define implícitamente a
define implícitamente a  e
e  como funciones de
como funciones de  . Hallar la ecuación de la recta tangente a la gráfica de
. Hallar la ecuación de la recta tangente a la gráfica de
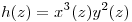 en
en 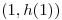
3) Sea 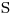 la superficie parametrizada por
la superficie parametrizada por
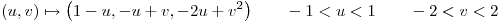
Hallar los 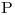 pertenecientes a
pertenecientes a 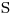 tales que el plano tangente a
tales que el plano tangente a 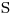 en
en 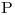 es paralelo al vector
es paralelo al vector 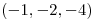 .
.
4) Sea 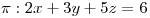 el plano tangente a la gráfica de
el plano tangente a la gráfica de 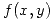 en
en 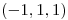 y sea
y sea 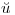 un versor tangente a la curva de nivel 9 de
un versor tangente a la curva de nivel 9 de 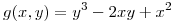 en
en  . Hallar la derivada direccional de
. Hallar la derivada direccional de  en
en 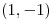 en la dirección del
en la dirección del 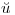 elegido.
elegido.
5) Sea 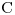 la curva en
la curva en 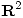 parametrizada por
parametrizada por
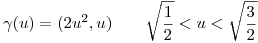
Sea 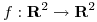 definida por
definida por 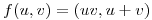
Mostrar que la imagen por  de la curva
de la curva  en el punto
en el punto  es perpendicular a la recta
es perpendicular a la recta 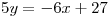 .
.
Resolución
Punto V
Metés a 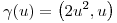 adentro de
adentro de 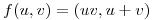 , o sea, armás la composición.
, o sea, armás la composición.
A vos te piden la imagen por  de
de  en
en  , o sea que
, o sea que 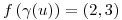 .
.
La composición queda 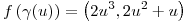 .
.
Hacés el despeje y te da que  .
.
Ahora buscás el vector director de la recta tangente en ese punto, así que derivás: 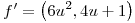
Metés  y el vector te da
y el vector te da 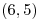 .
.
Resulta que te pedían que muestres que era perpendicular con la recta 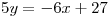 , o sea que el PI de los directores tiene que ser 0.
, o sea que el PI de los directores tiene que ser 0.
Parametrizamos la recta: 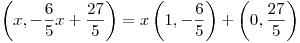 .
.
Ahí va el PI:
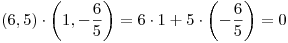
Y mostramos lo que nos pedían.
