Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: 1era Oportunidad - 2do Cuatrimestre 2007
Día: 03/11/2007
Enunciado
- Sea
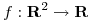 una función
una función 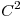 tal que
tal que 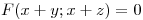 define implicitamente
define implicitamente 
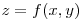 en un entorno de
en un entorno de 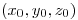 Verificar que en
Verificar que en 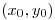 se cumple que
se cumple que 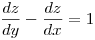
- Sea
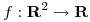 una función
una función 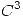 y el polinomio de Taylor de grado 2 de
y el polinomio de Taylor de grado 2 de 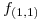 es
es
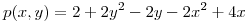 hallar a para que la función
hallar a para que la función
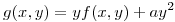 tenga un extremo en
tenga un extremo en  y determinar si es mínimo o maximo.
y determinar si es mínimo o maximo.
- Hallar la ecuación de la recta tangente a la curva descrita en coordenadas polares por:
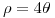 en
en 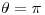
- Dada la superficie
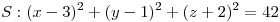 y las rectas:
y las rectas:
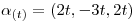 y
y 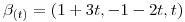 encontrar los puntos de S.
Para los que el plano tangente a S en dichos puntos sea paralelo a ambas rectas, hallar las ecuaciones de dichos planos
encontrar los puntos de S.
Para los que el plano tangente a S en dichos puntos sea paralelo a ambas rectas, hallar las ecuaciones de dichos planos
- Hallar todos los valores de a,b,c tales que la derivada direccional de
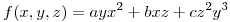 en
en 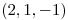 :
:
- Alcance su valor maximo en direccion paralela al eje

- Dicho valor sea
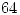
Resolución
Punto I
Siendo 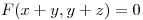 , tomo
, tomo 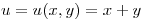 ,
, 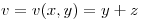 , y entonces queda
, y entonces queda 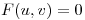 . Haciendo un diagrama en árbol y aplicando la regla de la cadena queda que:
. Haciendo un diagrama en árbol y aplicando la regla de la cadena queda que:
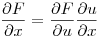
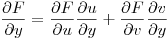
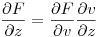
Derivando u y v, siempre dentro del entorno pedido:
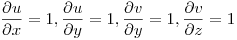 Después se aplica Cauchy-Dini para calcular
Después se aplica Cauchy-Dini para calcular 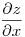 y
y 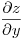 , se lo reemplaza en la ecuación dada y se verifica.
, se lo reemplaza en la ecuación dada y se verifica.
Punto II
Como 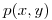 es el polinomio de Taylor de
es el polinomio de Taylor de 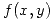 en
en  , tiene que cumplir que:
, tiene que cumplir que:
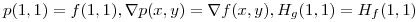 , sacando las derivadas parciales de
, sacando las derivadas parciales de 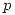 obtengo los datos de
obtengo los datos de  . Luego saco el gradiente de
. Luego saco el gradiente de  y lo igualo al vector
y lo igualo al vector 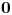 , exigiendo que se cumpla en el
, exigiendo que se cumpla en el  , creo que A me daba
, creo que A me daba 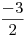 , armo la Hessiana de
, armo la Hessiana de  y me quedó que se alcanza un máximo en ese punto.
y me quedó que se alcanza un máximo en ese punto.
Punto III
Este es otro ejercicio que me salió muy facil y por eso tengo dudas de que esté bien hecho.
Pase de coordenadas polares a cartesianas
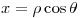
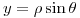 Reemplazo
Reemplazo 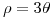 en
en  e
e  y parametrizo la curva:
y parametrizo la curva:
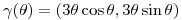 Derivo para sacar el vector tangente a la curva:
Derivo para sacar el vector tangente a la curva:
 Evaluando
Evaluando 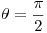 en gama tengo el punto de paso, y en la derivada de gama tengo la direccion de la recta y listo.
en gama tengo el punto de paso, y en la derivada de gama tengo la direccion de la recta y listo.
Punto IV
Defino la superficie  en forma implícita, para sacar el gradiente que por propiedad es perpendicular al plano tangente a
en forma implícita, para sacar el gradiente que por propiedad es perpendicular al plano tangente a  , y lo puedo usar como vector normal. Saco los vectores directores de las rectas derivando. Para que cumpla con lo pedido, la normal del plano tangente debe ser perpendicular a los dos vectores tangentes a las rectas, lo consigo haciendo el producto cruz, e igualandolo a una cte por la normal (porque tiene que ser un vector paralelo a la normal), haciendo las cuentas que ni da para escribirlas, queda
, y lo puedo usar como vector normal. Saco los vectores directores de las rectas derivando. Para que cumpla con lo pedido, la normal del plano tangente debe ser perpendicular a los dos vectores tangentes a las rectas, lo consigo haciendo el producto cruz, e igualandolo a una cte por la normal (porque tiene que ser un vector paralelo a la normal), haciendo las cuentas que ni da para escribirlas, queda  como variable independiente (aguante el rojo! cuak),
como variable independiente (aguante el rojo! cuak),  depende de
depende de  ,
,  depende de
depende de  . Reemplazo estos valores en la ecuación de
. Reemplazo estos valores en la ecuación de  y obtengo los puntos, que son dos, saco las normales en esos puntos y armo el plano tangente.
Creo que el desarrollo esta bien pero me dio un montón de raíces de
y obtengo los puntos, que son dos, saco las normales en esos puntos y armo el plano tangente.
Creo que el desarrollo esta bien pero me dio un montón de raíces de  .
.
Punto V
Derivo a  respecto de
respecto de  ,
,  y
y  . Como las derivadas parciales son continuas, entonces
. Como las derivadas parciales son continuas, entonces  es diferenciable, entonces puedo definir a la derivada direccional como
es diferenciable, entonces puedo definir a la derivada direccional como  , y empiezo a sacar las condiciones, la dirección tiene que ser máxima, y esto se logra en la dirección del vector gradiente por propiedad, dicha dirección tiene que ser unitaria por eso hay que normalizar al gradiente, tiene que ser paralela al eje
, y empiezo a sacar las condiciones, la dirección tiene que ser máxima, y esto se logra en la dirección del vector gradiente por propiedad, dicha dirección tiene que ser unitaria por eso hay que normalizar al gradiente, tiene que ser paralela al eje  , o dicho de otro modo paralela al vector
, o dicho de otro modo paralela al vector  , con esto saque
, con esto saque  y
y  , luego la derivada direccional la igualo a
, luego la derivada direccional la igualo a 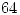 y saco
y saco  .
.
