Parcial – 61.03. Análisis Matemático – 19/10/06 - TEMA 2
Cátedra: Sirne
Fecha: 1º Oportunidad - (2º Cuatrimestre) TEMA 2
Día: 19/10/2006
Enunciado
1. Hallar la máxima distancia al origen de los puntos sobre la curva de ecuación 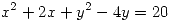 . Interpretar geométricamente.
. Interpretar geométricamente.
2. La máxima derivada direccional de una función 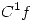 en
en 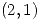 vale 5, y
vale 5, y 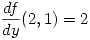 . Hallar
. Hallar 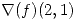 sabiendo además que
sabiendo además que 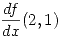 es positiva.
es positiva.
3. Sea  la curva parametrizada por
la curva parametrizada por 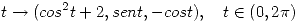 . Hallar todos los puntos
. Hallar todos los puntos  en los que su plano normal es paralelo al plano
en los que su plano normal es paralelo al plano  .
.
4. Resolver y fundamentar brevemente su respuesta
(a) ¿En qué puntos de la superficie de ecuación 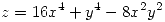 es su plano tangente horizontal?
es su plano tangente horizontal?
(b) Dada una función 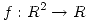 tal que
tal que 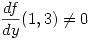 y
y 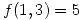 , sea
, sea 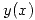 la función definida por la ecuación
la función definida por la ecuación 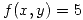 en un entorno de
en un entorno de 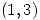 a la curva de ecuación
a la curva de ecuación 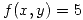 hallar y'(1).
hallar y'(1).
5. Sea  la superficie parametrizada por
la superficie parametrizada por
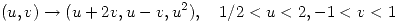 Hallar un vector tangente en
Hallar un vector tangente en 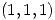 a la intersección de
a la intersección de  con el plano de ecuación
con el plano de ecuación 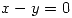 .
.
Resolución
