Examen (Parcial) - 61.03. Análisis Matemático II
Cátedra: Sirne/12
Fecha: 1er Oportunidad - (2do Cuatrimestre) 2006
Día: 19/10/2006
Enunciado
- Hallar la máxima distancia al origen de los puntos sobre la curva de ecuación
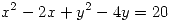 .Interprete gráficamente.
.Interprete gráficamente. - La máxima derivada direccional de una función
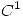
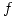 en
en  vale 4, y
vale 4, y 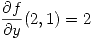 . Hallar
. Hallar 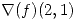 sabiendo además que
sabiendo además que 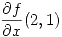 es positiva.
es positiva. - Sea
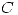 la curva parametrizada por
la curva parametrizada por 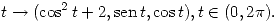 Hallar todos los puntos de
Hallar todos los puntos de 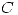 en los que su plano normal es paralelo al plano
en los que su plano normal es paralelo al plano 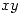 .
. - Resolver y fundamentar brevemente su respuesta
- ¿En qué puntos de la superficie de educación
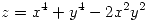 es su plano tangente horizontal?
es su plano tangente horizontal? - Dada una función
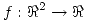 tal que
tal que 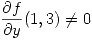 y
y 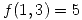 , sea
, sea 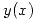 la función definida por la ecuación
la función definida por la ecuación 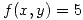 en un entorno de
en un entorno de 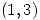 . Sabiendo que el vector
. Sabiendo que el vector 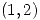 es tangente en
es tangente en 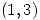 a la curva de ecuación
a la curva de ecuación 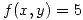 , hallar
, hallar 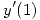 .
.
- Sea
 la superficie parametrizada por
la superficie parametrizada por 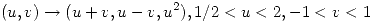
Hallar un vector tangente en 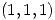 a la intersección de
a la intersección de  con el plano de ecuación
con el plano de ecuación 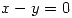 .
.
Resolución
Punto II
El valor de la derivada direccional de una función C1 en determinado punto esta dada por la norma del vector que determina esta dirección.
La derivada direccional máxima de una función C1 en un punto esta dada por su gradiente.
Con lo dicho se puede interpretar la primer frase del enunciado como 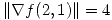 (1)
(1)
El gradiente está compuesto por las derivadas parciales con respecto a sus variables:
![<tex>\| \nabla f (2,1) \| = \left[ \frac{\partial f}{\partial x} (2,1) , \frac{\partial f}{\partial y} (2,1) \right]</tex> <tex>\| \nabla f (2,1) \| = \left[ \frac{\partial f}{\partial x} (2,1) , \frac{\partial f}{\partial y} (2,1) \right]</tex>](lib/plugins/latex/images/230687cc5ddde8b9e39c689e3f1957512761d87b_0.png)
Pero por el dato del enunciado sabemos que 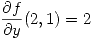
Por (1) podemos escribir:
![<tex> \sqrt { \left[\frac{\partial f}{\partial x} (2,1)\right]^2 + 2^2 } = 4 </tex> <tex> \sqrt { \left[\frac{\partial f}{\partial x} (2,1)\right]^2 + 2^2 } = 4 </tex>](lib/plugins/latex/images/af0ba77f555046fe44f3ad821936ff87244d4adc_0.png)
entonces…
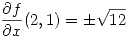
Se pide el valor positivo de 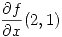 por lo tanto el gradiente pedido es:
por lo tanto el gradiente pedido es:
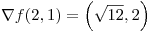
Punto III
Se pide que el plano tangente sea paralelo al xy, lo cual equivale a pedir que su vector normal tenga la siguiente estructura:
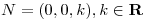 (1)
(1)
La dirección normal al plano normal de una curva es la misma que la de su vector tangente en ese punto. El vector tangente a una curva puede obtenerse derivando cada componente de su expresión parametrizada:
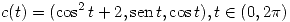
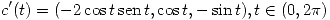
Por lo dicho en (1) necesitamos que:
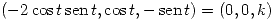
Igualamos componente a componente:
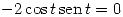
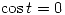
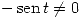
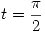 y
y 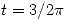 cumplen lo pedido.
cumplen lo pedido.
Entonces los puntos de 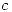 en los cuales su plano normal es paralelo al
en los cuales su plano normal es paralelo al 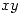 son:
son:
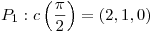 y
y 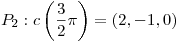
Punto IV
Parte A
El ejercicio nos pide los puntos donde el plano tangente a la superficie dada, es horizontal, esto es decir
que debe ser paralelo al plano 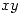 o lo que es equivalente tener como normal un vector de la forma
o lo que es equivalente tener como normal un vector de la forma 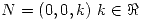
Y para obtener la normal de la superficie 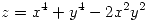 redefinimos la funcion dada como
redefinimos la funcion dada como
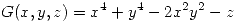 y elegimos la superficie de nivel 0 de esta funcion, de esta forma
podemos decir que
y elegimos la superficie de nivel 0 de esta funcion, de esta forma
podemos decir que 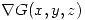 sera perpendicular a la superficie de nivel que tenemos punto
a punto (que es igual a la que nos dieron de dato).
sera perpendicular a la superficie de nivel que tenemos punto
a punto (que es igual a la que nos dieron de dato).
Con lo cual obtenemos la normal del plano a la que debemos aplicar la restriccion antes encontrada.
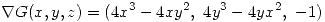
Aplicamos la restriccion haciendo:
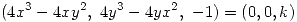
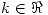
con esto deducimos :
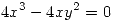 (1)
(1)
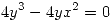 (2)
(2)
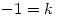 (3)
(3)
de 1 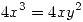 haciendo la aclaracion
haciendo la aclaracion 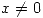 despejamos
despejamos 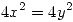 y de ahi despejamos
y de ahi despejamos 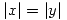 de 2
de 2 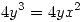 haciendo la aclaracion
haciendo la aclaracion  despejamos
despejamos  y obtenemos
y obtenemos 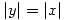 que es equivalente a lo obtenido en 1.
que es equivalente a lo obtenido en 1.
Analizamos ahora el caso de  e
e 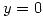 .
.
Primero reemplazamos  en las ecuaciones. En 1 no obtengo informacion, en 2 obtengo
en las ecuaciones. En 1 no obtengo informacion, en 2 obtengo
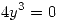 osea que cuando
osea que cuando  se debe cumplir que
se debe cumplir que 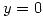 .
Luego reemplazamos
.
Luego reemplazamos 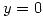 en las ecuaciones. En 2 no obtengo informacion, en 1 obtengo
en las ecuaciones. En 2 no obtengo informacion, en 1 obtengo
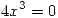 osea que cuando
osea que cuando 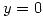 se debe cumplir que
se debe cumplir que  , que es compatible con la info obtenida anteriormente.
, que es compatible con la info obtenida anteriormente.
Obtuvimos que los puntos que cumplen las condiciones impuestas son los puntos de los planos 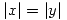 osea
osea
 y
y 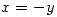 incluyendo el caso
incluyendo el caso  e
e 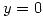 .
Reemplazo ahora en la ecuacion de la superficie, (por que conocemos los puntos que cumplen, ahora de ellos, debemos encontrar los que estan en la superficie dada).
.
Reemplazo ahora en la ecuacion de la superficie, (por que conocemos los puntos que cumplen, ahora de ellos, debemos encontrar los que estan en la superficie dada).
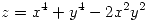 reemplazo
reemplazo  me da
me da 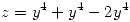 ,
,
 , usando
, usando 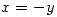 tambien tengo
tambien tengo  .
.
Entonces la solucion del problema son los puntos de las rectas:
 ,
,  y
y
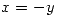 ,
,  .
.
