Tabla de Contenidos
Parcial - 61:03. Análisis Matemático II – 27/05/06 - TEMA 2
Cátedra: Acero
Fecha:27/05/06 2º Oportunidad – 1º Cuatrimestre
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Sea
 la curva en
la curva en 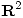 de ecuación
de ecuación 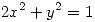 . Hallar una dirección tangente a
. Hallar una dirección tangente a  en
en 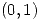 de manera que la derivada direccional de
de manera que la derivada direccional de 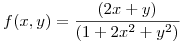 en
en 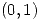 en esa dirección sea positiva.
en esa dirección sea positiva. - Hallar
 de manera que la recta de ecuaciones
de manera que la recta de ecuaciones 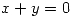 ,
, 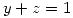 sea tangente en
sea tangente en 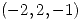 a la superficie parametrizada por
a la superficie parametrizada por 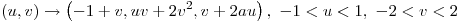 .
. - Sean
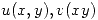 definidas por el siguiente sistema de ecuaciones
definidas por el siguiente sistema de ecuaciones
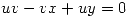
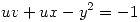 en el entorno de
en el entorno de 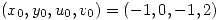 . Si
. Si 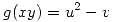 , calcular aproximadamente
, calcular aproximadamente 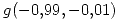 .
.
- Resolver y fundamentar brevemente su respuesta
- (a)Hallar los máximos y mínimos de
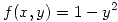 restringida a la curva de ecuación
restringida a la curva de ecuación 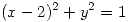 . Graficar.
. Graficar. - (b)Construir una función
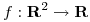 de clase
de clase 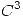 tal que su polinomio de Taylor de grado 2 en
tal que su polinomio de Taylor de grado 2 en 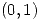 sea
sea
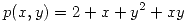 y
y 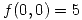 .
.
- Hallar todos los
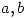
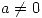 tales que
tales que
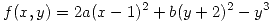 tiene extremo en
tiene extremo en  .
.
Resolución
- 1.
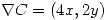
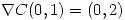 El vector tangente es perpendicular al gradiente entonces si los multiplico tiene que dar 0.
El vector tangente es perpendicular al gradiente entonces si los multiplico tiene que dar 0.
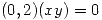
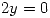
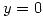
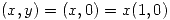
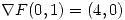
La derivada direccional tiene que ser mayor a 0:
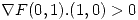
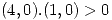
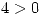
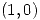 es una dirección en donde la derivada de
es una dirección en donde la derivada de 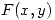 es positiva y además
es positiva y además 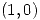 es un vector tangente a
es un vector tangente a  en
en 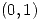 .
.
* 2.
 .
.
- 5.
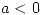
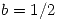 .
.
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
