[[Enunciado]]
Enunciado
- Sea C la curva de ecuaciones en coordenadas polares
 . Graficar C y hallar una ecuación para su recta tangente en
. Graficar C y hallar una ecuación para su recta tangente en  .
. - Hallar la intersección de la superficie parametrizada por
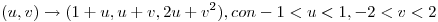
con su plano tangente en (1,0,0). - Sea
 una función
una función  con mínimo local en (0,2). Hallar la máxima derivada direccional de
con mínimo local en (0,2). Hallar la máxima derivada direccional de
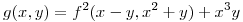
en (1,1) - Resolver y fundamentar brevemente su respuesta
- (a) Construír una función
 tal que tenga un mínimo en todos los puntos de la recta de ecuación x + y = 1.
tal que tenga un mínimo en todos los puntos de la recta de ecuación x + y = 1. - (b) Hallar los puntos más cercanos al origen en la curva de ecuación
 .
.
- Dada
 una función
una función  tal que F(0,2,2)=0 y
tal que F(0,2,2)=0 y  , sea
, sea  la superficie de ecuación F(x,y,z) = 0. Sea
la superficie de ecuación F(x,y,z) = 0. Sea  la superficie parametrizada por
la superficie parametrizada por

Si C es la curva de intersección de y
y  , hallar aproximadamente la intersección de C con el plano de ecuación z = 1,9.
, hallar aproximadamente la intersección de C con el plano de ecuación z = 1,9.
Resolución
- Paso de coordenadas polares a cartesianas, sabiendo que:
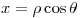
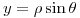
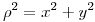
Para continuar hago un “truco” muy común cuando se trabaja en coordenadas polares:
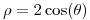
multiplico en ambos lados por y queda
y queda
 , comparando con las primeras expresiones
, comparando con las primeras expresiones
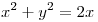
Paso el 2x para el otro lado y completo cuadrados
 ( Ec. de una circunferencia de radio 1 con centro en (1,0))
( Ec. de una circunferencia de radio 1 con centro en (1,0))
Parametrizo la curva
 con
con 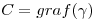
Luego el vector director de la recta tangente es la derivada
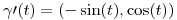
Busco la preimagen en el punto pedido:
 y
y 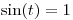
obtengo que
 , y el vector director será
, y el vector director será  , Luego la recta tangente queda
, Luego la recta tangente queda 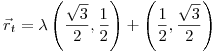
- Siendo la superficie S parametrizada por
 hallo la preimagen en el (1,0,0) y me queda que u = 0 y v = 0, los cuales pertenecen a los intervalos pedidos. Luego necesitamos el vector normal a la superficie que será perpendicular tanto al vector tangente dada por la curva u = cte como al vector tangente dada por la curva v = cte. Osea
hallo la preimagen en el (1,0,0) y me queda que u = 0 y v = 0, los cuales pertenecen a los intervalos pedidos. Luego necesitamos el vector normal a la superficie que será perpendicular tanto al vector tangente dada por la curva u = cte como al vector tangente dada por la curva v = cte. Osea  .
.


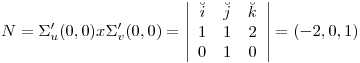
Luego la ecuación del plano tangente está dado por
![<tex> \Pi : N(X-P)=0 \\ (-2,0,1)[(x-1), y, z]=0 \\ z = 2(x-1) </tex> <tex> \Pi : N(X-P)=0 \\ (-2,0,1)[(x-1), y, z]=0 \\ z = 2(x-1) </tex>](lib/plugins/latex/images/7ad6db784e96a9d0091cfedfd8a571bdf4d97c54_0.png)
Busco la intersección de 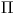 con
con 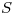
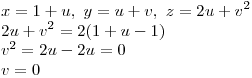
La intersección es:
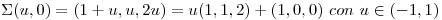
que no es mas que la ecuación de un segmento.
Nota: Aunque sea un detalle vale mencionar, fijense que no es lo mismo S que 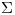 , sino que S es la supeficie en si, es decir la grafica, mientras que
, sino que S es la supeficie en si, es decir la grafica, mientras que 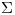 es la parametrización de S:
es la parametrización de S: 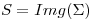
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

