Tabla de Contenidos
Examen Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: Segundo Recuperatorio - Segundo Cuatrimestre 2005
Día: 13/12/2005
Tema: 3
Esta página está incompleta; podés ayudar completando el material.
Enunciado
Punto I
Sea  la superficie parametrizada por
la superficie parametrizada por 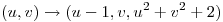 ,
, 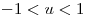 ,
, 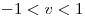 . Mostrar que todas las rectas normales a
. Mostrar que todas las rectas normales a  cortan la recta de ecuaciones
cortan la recta de ecuaciones  ,
, 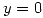 .
.
Punto II
Sea 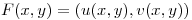 , con
, con 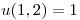 ,
, 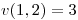 , una función
, una función  de
de 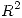 en
en 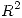 con matriz jacobiana
con matriz jacobiana
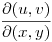 =
=
![<tex>\left[ \begin{array}{cc} 2x & 2y \\ 4x & -2y \end{array} \right]</tex> <tex>\left[ \begin{array}{cc} 2x & 2y \\ 4x & -2y \end{array} \right]</tex>](lib/plugins/latex/images/8faa4ccf6806dbcabc0e094e2689f4cf99995370_0.png)
y sea 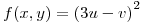 . Calcular
. Calcular  .
.
Punto III
Sea 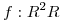
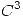 tal que su polinomio de Taylor de grado 2 en
tal que su polinomio de Taylor de grado 2 en  es
es 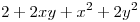 , y sea
, y sea 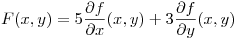
- Hallar
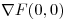 .
. - Si
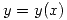 es la función definida implícitamente por
es la función definida implícitamente por 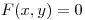 en un entorno de
en un entorno de 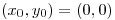 , hallar
, hallar 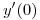 .
.
Punto IV
Resolver y fundamentar brevemente su respuesta:
- Sabiendo que el vector
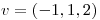 es tangente a la curva
es tangente a la curva  parametrizada por
parametrizada por 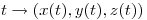 ,
, 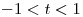 en
en 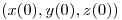 , hallar un vector tangente a la proyección de
, hallar un vector tangente a la proyección de  en el plano
en el plano  en el punto
en el punto 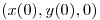 .
. - Mostrar un ejemplo de una función
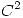 tal que restringida a
tal que restringida a  tenga máximo local estricto en
tenga máximo local estricto en 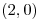 y restringida a
y restringida a 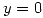 tenga mínimo local estricto en
tenga mínimo local estricto en 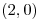
Punto V
Hallar los extremos de 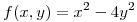 restringida a la curva de ecuaciones
restringida a la curva de ecuaciones 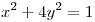 . Interpretar geométricamente.
. Interpretar geométricamente.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
