Examen Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: Primer Parcial - Segundo Cuatrimestre 2005
Día: 15/10/2005
Tema: 4
Enunciado
Punto I
Sea  la superficie en
la superficie en 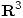 de ecuación
de ecuación 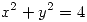 . Hallar los puntos
. Hallar los puntos  en
en  tales que la recta normal a
tales que la recta normal a  en
en  pasa por
pasa por  .
.
Punto II
Sabiendo que el plano tangente en 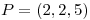 al gráfico de una función
al gráfico de una función 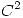
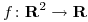 , tal que
, tal que 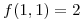 , es paralelo al plano de ecuación
, es paralelo al plano de ecuación 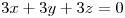 , hallar una ecuación de la recta tangente en
, hallar una ecuación de la recta tangente en  a la curva en
a la curva en 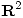 de ecuación
de ecuación 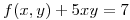 .
.
Punto III
Sea 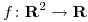 una función
una función 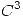 con mínimo local en
con mínimo local en 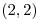 con
con 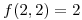 , con matriz Hessiana:
, con matriz Hessiana:
![<tex>H(f)(2,2) = \left[ \begin{array}{cc} 2 & 2 \\ 2 & 3 \end{array} \right]</tex> <tex>H(f)(2,2) = \left[ \begin{array}{cc} 2 & 2 \\ 2 & 3 \end{array} \right]</tex>](lib/plugins/latex/images/ed43f915efc8ef033d07bd94b63db0d648442845_0.png)
Hallar  y
y  tales que
tales que
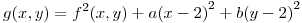
tenga máximo local en 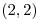
Punto IV
Resolver y fundamentar brevemente su respuesta:
- Sea
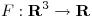 una función
una función 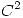 tal que
tal que 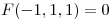 y
y 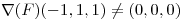 . Sabiendo que la recta normal a la superficie
. Sabiendo que la recta normal a la superficie  de ecuación
de ecuación 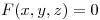 en
en 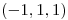 pasa por el origen, mostrar que
pasa por el origen, mostrar que  es tangente en
es tangente en 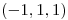 a la esfera de ecuación
a la esfera de ecuación 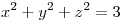
- Sea
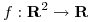
 tal que
tal que 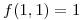 . Sabiendo que la superficie parametrizada por
. Sabiendo que la superficie parametrizada por
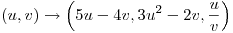 ,
, 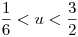 ,
, 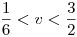
es tangente a la curva parametrizada por
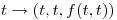 ,
, 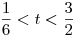
en 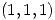 , calcular la derivada direccional
, calcular la derivada direccional 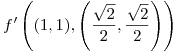
Punto V
Hallar, si existen, los extremos de  restringida al arco de curva descripto por
restringida al arco de curva descripto por 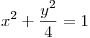 ,
,  . Interpretar geométricamente.
. Interpretar geométricamente.
Resolución
