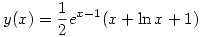Parcial - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: 2da Oportunidad - 1er Cuatrimestre 2004
Día: 01/06/2004
Enunciado
- Sea
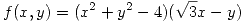
- Describir en coordenadas polares el conjunto
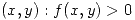
- Si
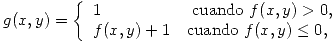
- Sean
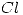 y
y 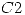 dos curvas parametrizadas respectivamente por
dos curvas parametrizadas respectivamente por 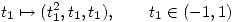 y por
y por 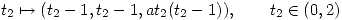
- Mostrar que las curvas se cortan en el punto
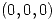 .
. - Hallar
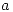 de manera que el corte de las curvas en
de manera que el corte de las curvas en 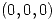 sea ortogonal.
sea ortogonal.
- Hallar todos los pares
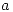 ,
, 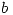 de números reales con
de números reales con 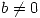 de manera que
de manera que 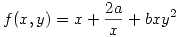 tenga un extremo local de valor 4, y para esos valores de
tenga un extremo local de valor 4, y para esos valores de 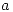 ,
, 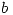 hallar todos los extremos de
hallar todos los extremos de 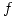 y clasificarlos.
y clasificarlos. - Sea
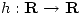 una función
una función 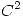 tal que
tal que 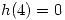 ,
, 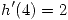 . Si la función
. Si la función 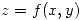 está definida implícitamente por la ecuación
está definida implícitamente por la ecuación 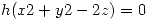 en un entorno de (2, 0, 0), calcular
en un entorno de (2, 0, 0), calcular 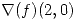 .
. - Sabiendo que el gráfico de una solución particular de la ecuación diferencial
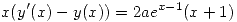 pasa por (1,1) y es paralelo en este punto a la recta de ecuación
pasa por (1,1) y es paralelo en este punto a la recta de ecuación 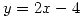 , hallar
, hallar 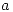 y la solución general de la ecuación.
y la solución general de la ecuación.
Resolución
Punto I
(I)
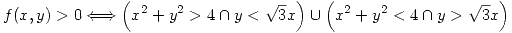
Gráfico:
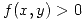
En coordenadas polares se expresa de la siguiente manera:
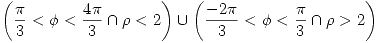
(II) Para analizar los puntos de discontinuidad de 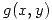 se deben tener en cuenta
se deben tener en cuenta 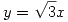 y en
y en 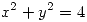 . Entonces:
. Entonces:
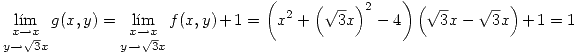
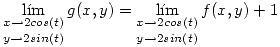
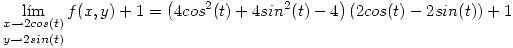
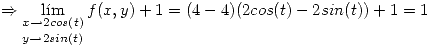
Punto II
(I) Si 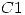 y
y 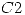 se cortan entonces existen un valor de
se cortan entonces existen un valor de 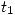 para
para 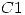 y un valor de
y un valor de 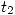 para
para 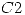 tal que
tal que 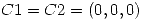 .
.
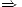 Se debe cumplir:
Se debe cumplir:
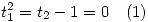
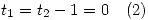

Se ve a simple vista que 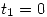 y
y 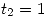 .
.
(II) Para que las dos curvas sean ortogonales se debe cumplir que la tangente de 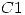 y la tangente de
y la tangente de 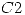 sean ortogonales en el punto (0,0,0). Para ello se deriva:
sean ortogonales en el punto (0,0,0). Para ello se deriva:
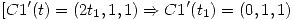
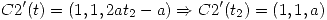
Entonces para que se corten ortogonalmente:
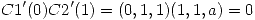
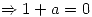

Punto III
Para resolver se utiliza el teorema de la función implícita. Sin embargo para poder aplicar dicho teorema se debe comprobar que:
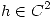
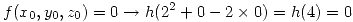
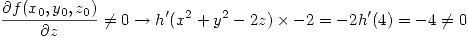
Con esto ya se puede aplicar el teorema. Entonces:
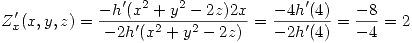
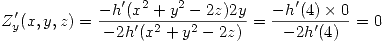
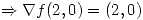
Punto IV
Lo primero que se hace es analizar las derivada respecto de 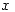 y de
y de 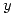 de la función con el objetivo de determinar los puntos críticos:
de la función con el objetivo de determinar los puntos críticos:
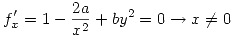
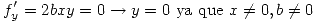
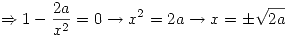
Puntos críticos: 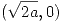 ,
, 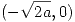
Para que haya extremo local de valor 4 se debe cumplir que 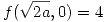
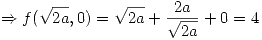
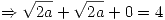
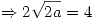
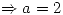
Entonces:
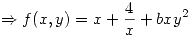
Se procede a obtener todos los extremos:
Puntos críticos: (-2,0), (2,0)
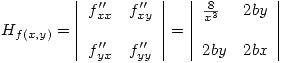

Si 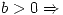 en
en 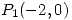 se alcanza un máximo local que es
se alcanza un máximo local que es 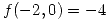
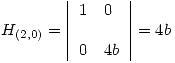
Si 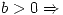 en
en 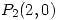 se alcanza un mínimo local que es
se alcanza un mínimo local que es 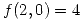
Punto V
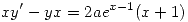
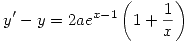
Para resolver dicha ecuación se emplea el método de Lagrange, donde 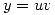 y
y 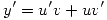
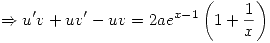
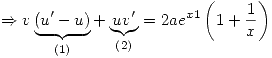
Se plantea 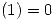 :
:
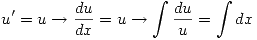
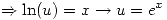
Reemplazando 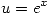 en
en 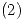 :
:
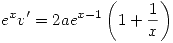
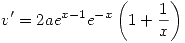
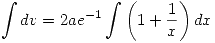
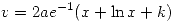
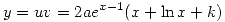
Como la solución pasa por (1,1) entonces 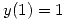
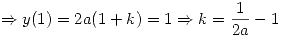
Por otro lado, sabiendo que la solución es paralela en el punto (1,1) a la recta de ecuación 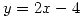 se deduce que
se deduce que 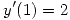
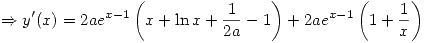
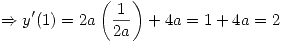
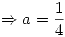
Habiendo obtenido los valores de 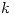 y de
y de 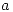 la solución queda de la siguiente manera:
la solución queda de la siguiente manera: