Plano tangente al gráfico de una función

Sea 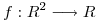, una función continua, derivable, macanuda y todas esas cosas que uno le pide para poder hacer el problema, y sea 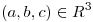un punto que reposa en la superficie 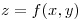(el gráfico de ), a continuación se detallan los pasos necesarios para obtener la ecuación del plano tangente al gráfico de en el punto :

1. Calcular el gradiente de la función , que al ser igualada a cero (¿o a una constante cualquiera?), define implícitamente a la superficie .
2. Evaluar en el punto . El resultado será la normal del plano tangente en ese punto.
3. Realizar el producto interno entre la normal del plano tangente y un vector genérico. La relación resultante, será la ecuación de un plano cuyos vectores generadores son idénticos a los del plano tangente.
4. A partir de aquí pueden obtenerse dichos generadores para luego sumarles el punto y conseguir la ecuación paramétrica del plano buscado.
5. Una alternativa al punto anterior es, reemplazar el 0 de la ecuación que se obtiene por un valor 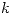genérico, y averiguar su valor sabiendo que el punto debe cumplir con dicha ecuación.

Cuando tenga más tiempo transcribo ésto: http://www.foros-fiuba.com.ar/viewtopic.php?p=130150#130150