Integral de superficie

Integral de superficie

La idea

La idea es una “explicación de café/bolsillo” sobre el asunto.

EL CONTENIDO AUN ES BORRADOR Y PUEDE CONTENER ERRORES SERIOS!

[FALTA: agregar imágenes aclaratorias]

Imaginemos que necesitamos conocer el área de un pedazo de superficie… Para eso, necesitamos: 1. una superficie 2. una curva ¹⁾ *sobre* la superficie que delimite la porcion que nos intereza (o sea, el borde).

La superficie puede existir en R2, R3, …, siendo su borde una curva de R2 o R3 o … Podemos definir una superficie de muchas formas, pero siempre buscaremos una parametrización porque: Es la forma más simple de laburar con la superficie, no causa grandes ruidos el cambiar de parametrización.

Ahora,

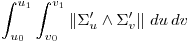$<tex> \int _{u_0}^{u_1} \int _{v_0}^{v_1} \left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\| \,du \,dv </tex>$ donde: u0 u1 son los límites del parametro u v0 v1 son los límites del parametro v

Cuidado: suele dar origen a muchos errores poner mal los límites de los parámetros, hay que tener mucho cuidado con eso .

Dado que una superficie requiere “dos niveles de libertad”, es logico qeu caigamos en integrales dobles (si se quiere, una por cada parámetro de la superficie).

En español el integrando es la norma del producto vectorial de las derivadas parciales de la paramétrica respecto de sus varaibles ( o sea, al 'vector' de la paramétrica, lo derivamos respecto del primer parámetro y luego del segundos, multiplicamos “esos vectores derivados” vectorialmente, y a ese vector le calculamos la norma).

Notación: para escribir esa integral de forma más compacta se usa una notación que declara “la paramétrica” (o sea, se usa la letra (sigma en general) en ves de poner dos barritas ²⁾ de integral con sus limites) $<tex> \int _{\Sigma} ,d \sigma </tex>$

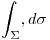
A jugar, paso 1

Imaginemos que a la integral anterior, al integrando, lo queremos multiplicar por algo… 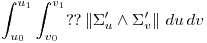$<tex> \int _{u_0}^{u_1} \int _{v_0}^{v_1} ?? \left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\| \,du \,dv </tex>$ [nota: sería lindo poder cambiar ?? por un cuadrado o un cuadrado con un ? adentro]

podemos multiplicarlo por un numero? Si. Si es una constante, no trae mucha diversión, pero es un primer paso. Dado qeu las “variables finales” de la integral son dos, podemos multiplicarlo por una función de esas variables… Pero no tiene mucha relación con la superficie… Bueno, dado que tenemos la paramétrica de la superficie, que a cada par (u,v) le da un puntito en la superficie, a cada puntito démosle un valor real (función de R2 a R o de R3 a r, depende de la superficie), y tenemos la composición de una función con la paramétrica de la superficie que da un numerito: $<tex> \int _{u_0}^{u_1} \int _{v_0}^{v_1} f ( \Sigma ( u , v ) ) \left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\| \,du \,dv </tex>$

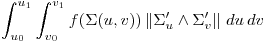
Notación: Lo anterior se escribe más compactamente: $<tex> \int _{\Sigma} f ,d \sigma </tex>$

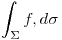
A jugar, paso 2

Ahora, dado que pudimos meter en la integral una función de varias variables, podríamos meter un campo de varias variables? ( o sea, algo que para cada punto de la superficie, no me de un punto, sino un vector)?

La pregunta sería: ¿cómo puedo hacer para de un vector obtener un numerito y caer en el caso anterior? ¿con qué cosa vectorial de la suèrficie puedo mexclarlo?

Podría simplemente usar la norma de f, pero eso, aunque posible, decae en el otro caso, no hay mucho vectorial en el medio.

Ahora, tal como usamos el producto interno para la integral de curva, podemos hacer el producto interior de la norma de cada punto de la superficie con el vector de f en ese punto.

Por tal nos queda: $<tex> \int _{u_0}^{u_1} \int _{v_0}^{v_1} \overline{f} ( \Sigma ( u , v ) ) \wedge \left( \frac{ \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} } {\left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\|} \right) * \left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\| \,du \,dv </tex>$

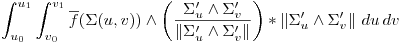
Simplificando: $<tex> \int _{u_0}^{u_1} \int _{v_0}^{v_1} \overline{f} ( \Sigma ( u , v ) ) \wedge ( \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} ) \,du \,dv </tex>$

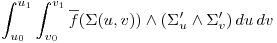
Cuidado: Dado que, el cambiar de sentido un vector cambia el signo del producto vectorial, es importante notar qeu NO es igual elegir una normal de la superficie o la que va en el otro sentido (la que sale o la que entra, la qeu sube o la qeu baja,…).

Notación: 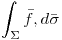$<tex> \int _{\Sigma} \bar f ,d \bar \sigma </tex>$ (notar que el sigma del diferencial tiene barra)

Nomenclatura: a esta integral se le llama Flujo (o más largo: flujo de F sobre una superficie)

¿para qué sirve la integral?

1- calcular el área de la superficie 2- calcular sobre la superficie el total de “una propiedad” de la misma (temperatura/masa en una placa,…) 3- calcular la componente perpendicular a la superficie de un vector, ejemplo cuánto volumen de un líquido pasó por una superficie (digamos un pedacito de red de pezcar).

Anexo1:

[HACER]de dónde sale la formulita de area de superficie.

Anexo2:

Resumen de ecuaciones: $<tex> \int _{\Sigma} ,d \sigma = \int _{u_0}^{u_1} \int _{v_0}^{v_1} \left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\| \,du \,dv </tex>$ $<tex> \int _{\Sigma} f ,d \sigma = \int _{u_0}^{u_1} \int _{v_0}^{v_1} f ( \Sigma ( u , v ) ) \left\| \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} \right\| \,du \,dv</tex>$ $<tex> \int _{\Sigma} \bar f ,d \bar \sigma = \int _{u_0}^{u_1} \int _{v_0}^{v_1} \overline{f} ( \Sigma ( u , v ) ) \wedge ( \Sigma^{\prime}_{u} \wedge \Sigma^{\prime}_{v} ) \,du \,dv</tex>$

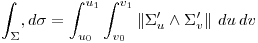
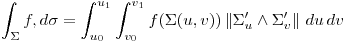
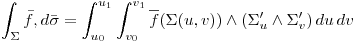
Ejemplos

[HACER]

¹⁾ evidentemente, estamos una curva cerrada

²⁾ o eses o vivoritas