Integral de linea

Integral de linea

La idea

La idea es una “explicación de café/bolsillo” sobre el asunto.

EL CONTENIDO AUN ES BORRADOR Y PUEDE CONTENER ERRORES SERIOS!

[FALTA: agregar imágenes aclaratorias]

Imaginemos que necesitamos conocer el largo de un pedazo de curva… Para eso, necesitamos: 1. una curva 2. un punto de la curva que oficie de uno de sus extremos 3. el otro punto de la curva que oficie del otro de los extremos

La curva puede existir en R2, R3, …, siendo sus extremos indicados como puntos de R2 o R3 o … Podemos definir la curva de muchas formas, pero siempre buscaremos una parametrización porque: Es la forma más simple de laburar con la curva, no causa grandes ruidos el cambiar de parametrización.

Dada una parametrización, los puntos de origen y fin del arco de curva, equivalen a sendos valores del parámetro que dan esos puntos. Con lo antedicho, la integral de linea que da la longitud de curva es:

$<tex> \int _{t_0}^{t_1} \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$

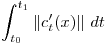
donde: t0 es el valor que en C(t0) nos da el punto de origen del segmento t1 es el valor que en C(t1) nos da el punto de final del segmento

Detalle: invertir t0 y t1 (origen y final) no cambia el valor de la integral (que calcula una longitud, no hay longitud negativa)

Notación: para escribir esa integral de forma más compacta se usa una notación que declara, los puntos de origen y final; la curva. $<tex> \int _{A}^{B} ds </tex>$

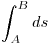
A jugar, paso 1

Imaginemos que a la integral anterior, al integrando, lo queremos multiplicar por algo…

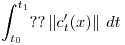$<tex> \int _{t_0}^{t_1} ?? \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$ [nota: sería lindo poder cambiar ?? por un cuadrado o un cuadrado con un ? adentro]

podemos multiplicarlo por un numero? Si, es una constante, no trae mucha diversión, pero es un primer paso. Dado qeu la “variable final” de la integral es t, podemos multiplicarlo por una función de t… Pero no tiene mucha relación con la curva… Bueno, dado que tenemos la paramétrica de la curva, que a cada t le da un puntito en la curva, a cada puntito démosle un valor real (función de R2 a R o de R3 a r, depende de la curva), y tenemos la composición de una función con la paramétrica de la curva que da un numerito:

$<tex> \int _{t_0}^{t_1} f(c(t)) * \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$

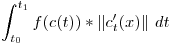
Dado que la integral “acumula” el largo de pedacitos de curva “ponderados” (multiplicados) por un numero, no cambia si invertimos los límites de integración.

Notación: Lo anterior se escribe más compactamente: $<tex> \int _{A}^{B} f ,ds </tex>$

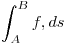
A jugar, paso 2

Ahora, dado que pudimos meter en la integral una función de varias variables, podríamos meter un campo de varias variables? ( o sea, algo que para cada punto de la curva, no me de un punto, sino un vector)?

La pregunta sería: ¿cómo puedo hacer para de un vector obtener un numerito y caer en el caso anterior? ¿con qué cosa vectorial de la curva puedo mexclarlo?

Podría simplemente usar la norma de f, pero eso, aunque posible, decae en el otro caso, no hay mucho vectorial en el medio.

Cada punto de la curva tiene su vector dirección tangente (el c'(t) ), por tal, ahí tengo otro vector (proveniente de la curva). Para qeu la cosa cierre, a c' lo dividimos por su norma. Puedo, hallar el producto interno de ambos vectores que vale para R2 y R3 y da un numerito :). ( y que es más general qeu el escalar qeu está solo en R3 y que da otro vector :S)

Por tal nos queda:

$<tex> \int _{t_0}^{t_1} f(c(t)) * c'(t)* / \left\| c^{\prime}_{t} (x) \right\| * \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$

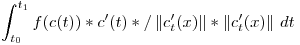
Simplificando:

$<tex> \int _{t_0}^{t_1} f(c(t)) * c'(t) \,dt </tex>$

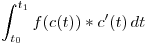
Dado que, el cambiar de sentido un vector cambia el signo del producto vectorial, invertir los limites de integracion (= cambiar el sentido de recorrido de la curva) cambia el signo de la integral

$<tex> \int _{t_0}^{t_1} f(c(t)) * c'(t) \,dt = - \int _{t_1}^{t_0} f(c(t)) * c'(t) \,dt </tex>$

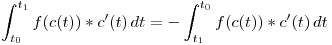
Notación: $<tex> \int _{A}^{B} \bar f ,d \bar s </tex>$

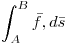
¿para qué sirve la integral?

1- calcular la longitud de curva 2- calcular sobre la curva el total de “una propiedad” de la misma (temperatura/masa en un hilo,…) 3- calcular la componente sobre la curva de un vector, típica definición del trabajo de una fuerza.

Anexo1:

[HACER]de dónde sale la formulita de long de curva.

Anexo2:

Resumen de ecuaciones: $<tex> \int _{A}^{B} ds = \int _{t_0}^{t_1} \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$ $<tex> \int _{A}^{B} f ,ds = \int _{t_0}^{t_1} f(c(t)) * \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$ $<tex> \int _{A}^{B} \bar f ,d \bar s = \int _{t_0}^{t_1} f(c(t)) * c^{\prime}_{t} (x) \,dt </tex>$

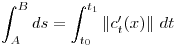
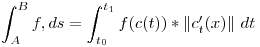
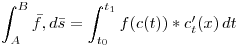
Cambio de signo: $<tex> \int _{A}^{B} f ,ds = \int _{B}^{A} f ,ds </tex>$ $<tex> \int _{t_0}^{t_1} f(c(t)) * \left\| c^{\prime}_{t} (x) \right\| \,dt= \int _{t_1}^{t_0} f(c(t)) * \left\| c^{\prime}_{t} (x) \right\| \,dt </tex>$

$<tex> \int _{A}^{B} \bar f ,d\bar s = - \int _{B}^{A} \bar f ,d\bar s </tex>$ $<tex> \int _{t_0}^{t_1} f(c(t)) * c^{\prime}_{t} (x) \,dt = - \int _{t_1}^{t_0} f(c(t)) * c^{\prime}_{t} (x) \,dt </tex>$

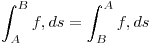
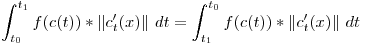
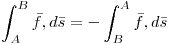
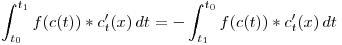
Lo mismo más visual

Ejemplos

[HACER]