Examen Final - 61.03. Análisis Matemático II - 19/12/2013
Cátedra: Todas
Fecha: Primer Oportunidad - Verano 2013
Día: 19/12/2013
Enunciado
Punto I
Hallar, analíticamente, la distancia mínima entre el punto  y la curva, contenida en el primer cuadrante, definida por la ecuación diferencial
y la curva, contenida en el primer cuadrante, definida por la ecuación diferencial 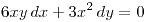 que pasa por el punto
que pasa por el punto 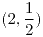 . Graficar la curva.
. Graficar la curva.
Punto II
Hallar el área de la porción de superficie descripta por 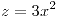 con
con  ,
, 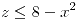 , en el primer octante.
, en el primer octante.
Punto III
Sea 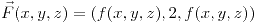 un campo vectorial
un campo vectorial 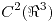 . Verificar que la circulación del campo a lo largo del perímetro del triángulo de vértices
. Verificar que la circulación del campo a lo largo del perímetro del triángulo de vértices  es nula.
es nula.
Punto IV
Hallar  y
y  de manera que el campo
de manera que el campo 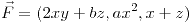 sea conservativo. Para los valores hallados calcular la circulación del campo a lo largo de la curva intersección de las superficies
sea conservativo. Para los valores hallados calcular la circulación del campo a lo largo de la curva intersección de las superficies  y
y 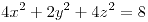 en el primer octante, desde
en el primer octante, desde 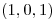 hasta
hasta 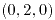 . Graficar las superficies y la curva.
. Graficar las superficies y la curva.
Punto V
Sea el campo vectorial 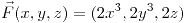 y
y  la superficie descripta por
la superficie descripta por 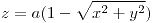 ,
,  . Hallar
. Hallar  de manera que el flujo de
de manera que el flujo de 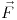 a través de
a través de  , orientada de manera que su normal tenga componente
, orientada de manera que su normal tenga componente  positiva, sea
positiva, sea  .
.
