materias:61:03:final_20090820_2 [Foros-FIUBA::Wiki]

1) Sean T campo escalar 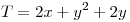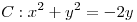$<tex>T= 2x + y^2 + 2y</tex>$ ; $<tex>C: x^2 + y^2 = -2y</tex>$ . Hallar extremos, graficar C y curvas de nivel de T en los extremos.

2) Hallar la familia de curvas tal que para todo $<tex>P(xo,yo)</tex>$ con x distinto de 0, la recta tg a $<tex>P</tex>$ en $<tex>Po</tex>$ corta al eje x en $<tex>(2xo,0)</tex>$

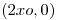
3) Sean A,B,C los puntos en los que el plano tangente de 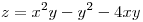$<tex>z=x^2y - y^2 - 4xy</tex>$ es paralelo al eje xy. Hallar A,B,C y la circulación de 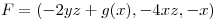$<tex>F = (-2yz +g(x), -4xz, -x)</tex>$ a través de ABC.

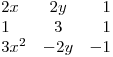4) Sea $<tex>F</tex>$ campo vectorial cuyo jacobiano es $<tex>\begin{array}{lcr}2x & 2y & 1\\1 & 3 & 1\\3x^2 & -2y & -1\end{array}</tex>$ , hallar la circulación de $<tex>F</tex>$ sobre la superficie $<tex>x^2+(y-1)^2+(z-3)^2 \leq 9</tex>$ .

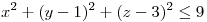5)Elegir una 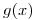$<tex>g(x)</tex>$ tal que la circulación de 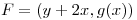$<tex>F=(y+2x, g(x))</tex>$ , sobre el paralelogramo de vértices 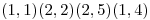$<tex>(1,1) (2,2) (2,5) (1,4)</tex>$ sea igual a 4