Examen Final - 61.03.Análisis Matemático II A - 17/02/2009
Día: 17/02/2009 Tema: II
Enunciado
Punto I
Sea 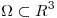 definida por
definida por 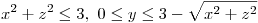 .
Calcular el flujo del campo
.
Calcular el flujo del campo 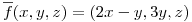 a través de la superficie del borde de
a través de la superficie del borde de 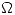 .
Indicar en un gráfico la dirección del vector normal elegido.
.
Indicar en un gráfico la dirección del vector normal elegido.
Punto II
Sea 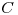 la curva definida por
la curva definida por 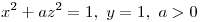 y
y 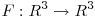 un campo
un campo 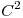 que satisface que
que satisface que 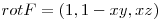 .
Hallar
.
Hallar 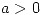 de manera que la circulación de
de manera que la circulación de 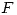 a lo largo de
a lo largo de 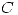 sea
sea 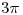 .
Orientar la curva de manera que en
.
Orientar la curva de manera que en 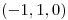 la tangente tenga coordenada
la tangente tenga coordenada  positiva.
positiva.
Punto III
Hallar la ecuación de la familia de curvas ortogonales a las curvas definidas por 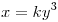 .
.
Punto IV
Si 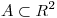 es una región de área 2, calcular el área de
es una región de área 2, calcular el área de 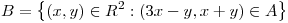
Punto V
Sea 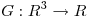 una función
una función  Calcular la circulación del campo
Calcular la circulación del campo
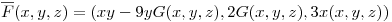 desde
desde 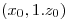 hasta
hasta 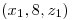 a lo largo de la curva
a lo largo de la curva 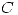 cuyos puntos pertenecen a la superficie de ecuación
cuyos puntos pertenecen a la superficie de ecuación 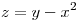 y su proyección sobre el plano
y su proyección sobre el plano  cumple con la ecuación
cumple con la ecuación 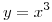 . Suponga
. Suponga 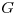 continua en
continua en 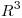
Resolución
Punto I
Tenemos a la Superficie 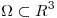 definida por
definida por 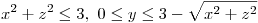
Se la parametriza:
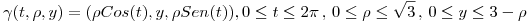
Es una superficie Cerrada Incluida en el Dominio de 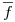 , y vemos q el campo vectorial
, y vemos q el campo vectorial 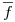 es
es 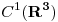
Podemos Aplicar el teorema de la Divergencia (o de Gauss), entonces nos quedaría lo siguiente:
Calculamos la 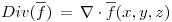 entonces nos queda:
entonces nos queda:
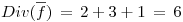
Apliquemos el Teorema de Gauss:
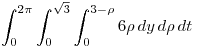
y me queda
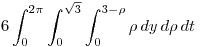
Operamos:
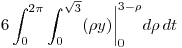
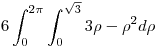
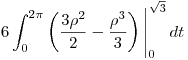
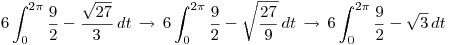
Operamos:
![<tex>6 [(\frac{9}{2}t - \sqrt{3}t) \bigg|_0^{2\pi}] \, = \, 6[ 9\pi - 2\sqrt{3}\pi] \, = \, 54\pi - 18\sqrt{3}\pi </tex> <tex>6 [(\frac{9}{2}t - \sqrt{3}t) \bigg|_0^{2\pi}] \, = \, 6[ 9\pi - 2\sqrt{3}\pi] \, = \, 54\pi - 18\sqrt{3}\pi </tex>](lib/plugins/latex/images/7e98398eb445d84e5b74f860bb8eb94433d8445a_0.png)
Por lo tanto
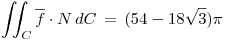
Punto II
tenemos la curva: 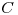 la curva definida por
la curva definida por 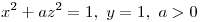
Parametrizo la curva:
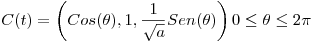 La Ree-parametrizamos para formar la superficie y nos queda:
La Ree-parametrizamos para formar la superficie y nos queda:
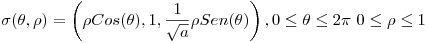
H1: El Campo Vectorial es 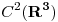
H2: La curva 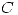 es un Lazo Simple de Jordan
es un Lazo Simple de Jordan
H3: La curva es el borde de la superficie 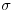
Cumplen las 3 hipotesis que requiere el Teorema de Stokes, entonces se lo puede aplicar:
La normal de la Superficie es 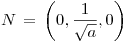
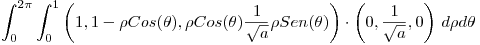
Resuelvo
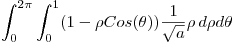
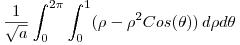
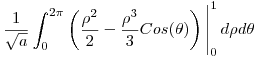
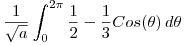
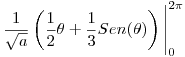
Ahora al resultado de toda esta porqueria se la iguala a 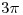
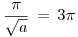
Operamos:
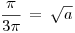
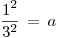 Entonces, el valor de a nos queda:
Entonces, el valor de a nos queda: