Examen Final - 61.03.Análisis Matemático II A - 16/07/2008
Tema: 1 Día: 16/07/2008
Enunciado
Punto I
Hallar la curva solucion de 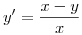 cuya recta tangente en el punto
cuya recta tangente en el punto 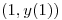 es paralela a la recta de ecuacion
es paralela a la recta de ecuacion 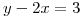 .
.
Punto II
Calcular la masa de la superficie cónica 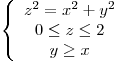 siendo la densidad en cada punto proporcional a su distancia al plano
siendo la densidad en cada punto proporcional a su distancia al plano 
Punto III
Hallar el volumen del cuerpo K definido por 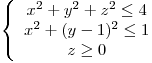
Punto IV
Sea 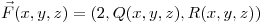 campo vectorial
campo vectorial 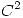 en
en 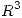 tal que
tal que 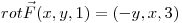 . Calcular la circulación del campo
. Calcular la circulación del campo 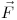 a lo largo de la curva C parametrizada por
a lo largo de la curva C parametrizada por 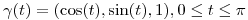 de forma que la tangente en cada punto tenga coordenada
de forma que la tangente en cada punto tenga coordenada  negativa.
negativa.
Punto V
Sea 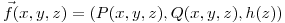 un campo vectorial
un campo vectorial 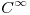 en
en 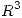 tal que
tal que 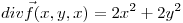 y
y 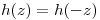 . Sea la superficie
. Sea la superficie 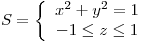 . Calcular el flujo de
. Calcular el flujo de 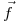 a través de
a través de  con la normal alejándose del eje z.
con la normal alejándose del eje z.
Resolución
Punto I
Tenemos la ecuacion diferencial 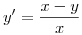 vamos a despejar un poco, “pasando” la
vamos a despejar un poco, “pasando” la  multiplicando a
multiplicando a 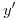
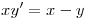 , pasamos la
, pasamos la  y nos queda formada la siguiente ecuacion diferencial
y nos queda formada la siguiente ecuacion diferencial 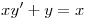 como podemos ver
como podemos ver 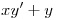 resulta ser la derivada de
resulta ser la derivada de ![<tex>[xy]'</tex> <tex>[xy]'</tex>](lib/plugins/latex/images/309cc1ac2ce147c3264d45f994eb0faaf61b5977_0.png) , entonces podemos transcribir a la ecuacion diferencial como
, entonces podemos transcribir a la ecuacion diferencial como ![<tex>[xy]'=x</tex> <tex>[xy]'=x</tex>](lib/plugins/latex/images/20c3696f57dbc524b1dce97153c191f085c1b296_0.png) ahora la primitiva de
ahora la primitiva de  tiene que ser la
tiene que ser la 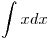 , es decir:
, es decir:
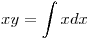 entonces
entonces 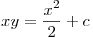 entonces nos queda q
entonces nos queda q 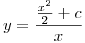 o bien
o bien 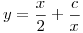 ahora me dicen q la recta tangente de la solución hallada tiene que ser paralela a la recta de ecuacion
ahora me dicen q la recta tangente de la solución hallada tiene que ser paralela a la recta de ecuacion 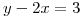 que la podemos transcribir como
que la podemos transcribir como 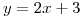 en el punto
en el punto 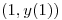 , y para que sean paralelas, tiene que tener igual pendiente, en este caso
, y para que sean paralelas, tiene que tener igual pendiente, en este caso  , derivemos la solucion de la ecuacion diferencial:
, derivemos la solucion de la ecuacion diferencial:
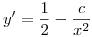 , ahora busquemos la pendiente de la recta tangente en el punto
, ahora busquemos la pendiente de la recta tangente en el punto 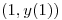 , donde aparecen las
, donde aparecen las  reemplazamos por
reemplazamos por  y a la
y a la 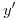 por
por  , es decir:
, es decir:
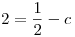 y nos queda q
y nos queda q 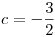
por lo tanto la solucion de la ecuacion diferencial nos queda como  , para ir redondeando el tema buscamos el valor de
, para ir redondeando el tema buscamos el valor de 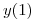 :
:
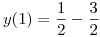 por lo tanto
por lo tanto 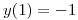 para finalizar:
para finalizar:
La solucion de la ecuacion diferencial 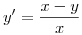 cuya recta tangente sea paralela en el punto
cuya recta tangente sea paralela en el punto 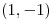 a la recta
a la recta 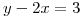 es:
es:

Punto II
Punto III
Punto IV
Punto V
Discusión
este final me lo envía Catalina L.
