Examen Final - 61.03.Análisis Matemático II A - 07/07/2008
Día: 07/07/2008
Enunciado
Punto I
Calcular el área de la porción de cono 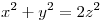 , interior al cilindo parametrizado por
, interior al cilindo parametrizado por 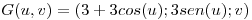 , con:
, con:
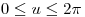 ,
,
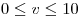
Punto II
Hallar y clasificar los extremos de la función 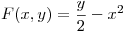 en la región:
en la región: 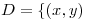 en
en 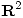 tales que:
tales que: 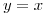 ,
, 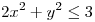 }
}
Punto III
Sean la curva 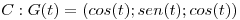 con
con 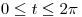 , y el campo
, y el campo 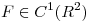 tal que:
tal que: 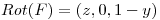 .
Calcular la circulación del campo
.
Calcular la circulación del campo  a lo largo de
a lo largo de 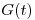 orientada de manera que su vector tangente en
orientada de manera que su vector tangente en 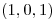 tenga coordenada positiva.
Sugerencia: Exprese
tenga coordenada positiva.
Sugerencia: Exprese 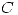 como intersección entre dos superficies.
como intersección entre dos superficies.
Punto IV
Sea 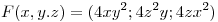 . ¿Qué radio debe tener una esfera centrada en el origen para que el flujo de
. ¿Qué radio debe tener una esfera centrada en el origen para que el flujo de  , hacia el exterior de dicha esfera, sea igual a 5 veces el volúmen de la misma?.
, hacia el exterior de dicha esfera, sea igual a 5 veces el volúmen de la misma?.
Punto V
Sea “sigma” la solución del problema de valor inicial:
![<tex>[ x^3+xy^2 ] dx + [ x^2y + y^3 ] dy = 0</tex> <tex>[ x^3+xy^2 ] dx + [ x^2y + y^3 ] dy = 0</tex>](lib/plugins/latex/images/81a4dc052e31391cbd630e5948d34912eeb80306_0.png) ; siendo
; siendo 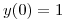 .
Calcular la circulación del campo:
.
Calcular la circulación del campo:
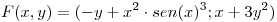 a lo largo de la curva “sigma” entre los puntos
a lo largo de la curva “sigma” entre los puntos 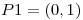 y
y 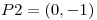 .
.
Resolución
Punto I
Punto II
Punto III
Punto IV
Punto V
Discusión
Disculpen lo horrible que es estar leyendo “equis cuadrado” como “x^2”, pero bueno, es lo que hay =P.
sacado del foro, posted by RiaNo.
