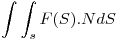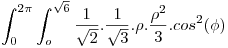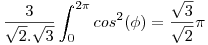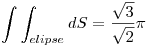Examen Final - 61.03. Análisis Matemático II A
Día: 04/03/2008
Enunciado
Punto I
Calcular la integral de linea del campo 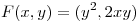 desde
desde 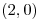 hasta
hasta 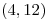 a lo largo de la curva
a lo largo de la curva  solucion particular de la ecuacion diferencial
solucion particular de la ecuacion diferencial 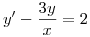 que pasa por dichos puntos.
que pasa por dichos puntos.
Punto II
Calcular el flujo del campo 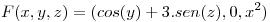 a traves del semielipsoide superior
a traves del semielipsoide superior 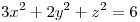 ,
,  considerando la normal de componente
considerando la normal de componente  positiva.
positiva.
Punto III
Sea el campo vectorial 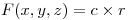 , donde
, donde  es un vector constante y
es un vector constante y  es el vector posicion. Demostrar que la circulacion de
es el vector posicion. Demostrar que la circulacion de  a lo largo de una curva cerrada simple y suave
a lo largo de una curva cerrada simple y suave 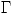 es proporcional al flujo de
es proporcional al flujo de  a traves de toda la superficie suave y orientable que tengo como borde a
a traves de toda la superficie suave y orientable que tengo como borde a 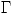
Punto IV
Describa en coordenadas cartesianas la region de 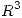 definida en coordenadas cilindricas por:
definida en coordenadas cilindricas por:
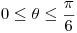
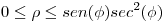
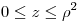
y calcule el volumen del cuerpo en las coordenadas que le parezca más convenientes.
Punto V
Hallar los extremos de 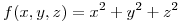 restringida a la curva dada por las ecuaciones:
restringida a la curva dada por las ecuaciones:
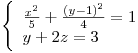
Resolución
Punto I
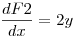
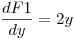
Como la matriz jacobiana de  es simetrica, entonces F es un campo conservativo. El resultado no depende del recorrido, solo del punto inicial y final.
es simetrica, entonces F es un campo conservativo. El resultado no depende del recorrido, solo del punto inicial y final.
Creo que recta que cumpla el 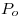 y el
y el 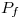
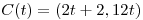 ,
, ![<tex>t \in [0,1]</tex> <tex>t \in [0,1]</tex>](lib/plugins/latex/images/2d7fe9925c088a81d16f913f06dabcb8f6e363b2_0.png)
Resuelvo la integral de linea:
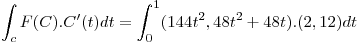
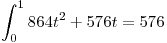
Punto II
Utilizo el teorema de la divergencia:
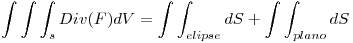
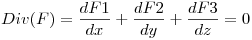
Entonces:
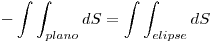
La integral sobre la superficie del plano es la mas facil de hacer, parametrizo el plano:
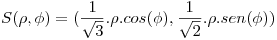
con : 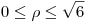 ,
, 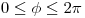
Calculo la normal:
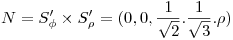
Resuelvo la integral con esta normal: