Examen Final - 61.03. Análisis Matemático II A
Día: 12/02/2008
Enunciado
Punto I
Sea 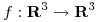 un campo vectorial
un campo vectorial  y
y  la curva parametrizada por:
la curva parametrizada por: 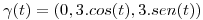 con
con ![<tex> t \in [0,\pi]</tex> <tex> t \in [0,\pi]</tex>](lib/plugins/latex/images/31f125d176c9576b10cde9cef7ceb2f132119841_0.png) .
Sabiendo que
.
Sabiendo que 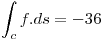 y que
y que 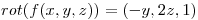 , calcular la integral de linea de
, calcular la integral de linea de
 a lo largo del eje
a lo largo del eje  desde
desde 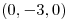 hasta
hasta 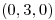 .
.
Punto II
Sean el campo vectorial 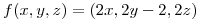 y
y  la superficie de potencial 5 del campo
la superficie de potencial 5 del campo  que pasa por
que pasa por 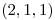 . Calcular el flujo de
. Calcular el flujo de  a traves de
a traves de  .
.
Punto III
Calcular la masa del cuerpo definido por: 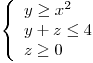 , si la densidad en cada punto es proporcional al producto de las distancias a los planos
, si la densidad en cada punto es proporcional al producto de las distancias a los planos 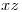 e
e 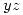 .
.
Punto IV
Sea el campo vectorial 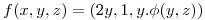 siendo
siendo 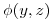 una funcion
una funcion  . Calcular el flujo de
. Calcular el flujo de  a traves de la superficie de ecuacion
a traves de la superficie de ecuacion  con
con 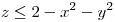 en el primer octante. Indique en un grafico la orientacion del vector normal que ha elegido
en el primer octante. Indique en un grafico la orientacion del vector normal que ha elegido
Punto V
Hallar la curva plana que pasa por 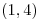 y satisface que en cada punto de cordenadas
y satisface que en cada punto de cordenadas  la recta tangente se interseca con el eje
la recta tangente se interseca con el eje  en un punto de ordenada
en un punto de ordenada 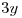
Resolucion
Punto I
No tenemos el campo vectorial, entonces aprovechamos el dato del rotor y aplicamos el teorema de Stokes.
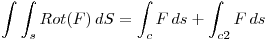
Parametrizo la superficie encerrada por la semicircunferencia y la recta:
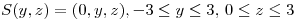
Saco la normal:

Como la normal es acorde a la circulacion, entonces se le deja el signo igual.
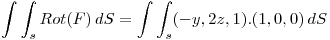
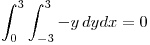
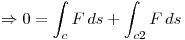
El enunciado nos da el dato : 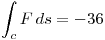
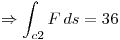
Punto II
Hay que buscar el potencial de 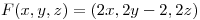
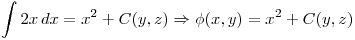
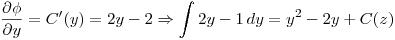

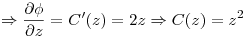
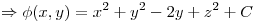
Nos dicen que tiene que pasar por el punto 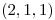
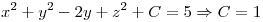
Entonces el equipotencial 5 nos queda:
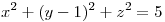 , Una esfera de radio
, Una esfera de radio 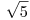
Por el teorema de la divergencia sabemos:
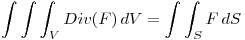
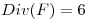
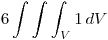
Como sabemos que la integral triple de 1 nos da el volumen, podemos utilizar la formula de volumen de la esfera:
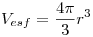
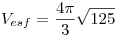
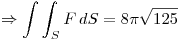
Punto III
La figura que se forma es una canaleta que se extiende en el eje  acotada por los planos
acotada por los planos  y
y 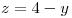 :
:
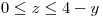
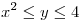
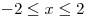
El enunciado nos dice que la densidad es:
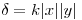
Son muy importante los modulos, sino el resultado da cero. Planteamos la integral triple:
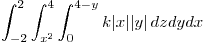
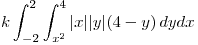
Como 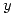 toma siempre valores positivos, puedo sacarle el modulo:
toma siempre valores positivos, puedo sacarle el modulo:
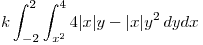
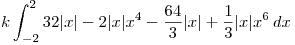
Para sacar el modulo vamos a tener que dividir la integral en dos partes:
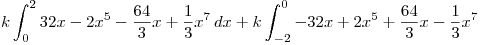
Haciendo las cuentas el resultado que nos da es :
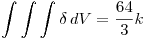
Punto IV
Parametrizo la superficie:
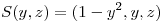
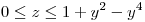
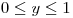
Busco la normal:
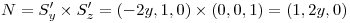
Calculo el flujo:
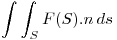
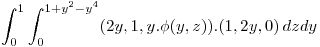
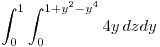
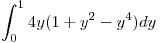
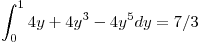
entonces:
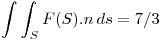
Punto V

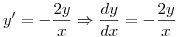
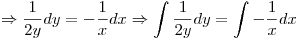
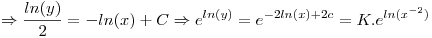
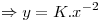
Ahora buscamos la solucion particular, reemplazo  por
por 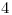 y
y  por
por  , y busco
, y busco 

