Examen Final - 61.03 Análisis Matemático II
Fecha: 3º Oportunidad - (1º Cuatrimestre Invierno) 2007
Día: 19/07/2007
Enunciado
Punto I
Se sabe que el campo vectorial 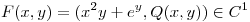 en
en 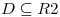 , siendo D la region definida en coordenadas polares por las siguientes ecuaciones:
, siendo D la region definida en coordenadas polares por las siguientes ecuaciones:
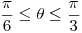
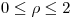
cuya frontera es la curva simple cerrada C. Justificar como debe elegirse 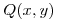 para que las circulaciones de
para que las circulaciones de 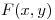 a lo largo de la curva
a lo largo de la curva 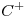 coincidan con el area de D.
coincidan con el area de D.
Punto II
Calcular el flujo de 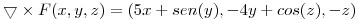 a traves de la superficie
a traves de la superficie 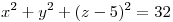 , con
, con  . Considere la normal con componente z positiva.
. Considere la normal con componente z positiva.
Punto III
Calcular la coordenada “y” del centro de masa de la placa de densidad 1 limitada por las curvas  ;
;  .
.
Punto IV
(a) Sea 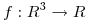 dada por
dada por 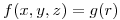 donde
donde 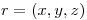 ,
, 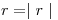 y
y 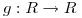 diferenciable. Calcule el flujo de
diferenciable. Calcule el flujo de 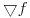 a traves de la porcion de cono
a traves de la porcion de cono 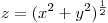 encerrada en el interior del cilindro de ecuación
encerrada en el interior del cilindro de ecuación 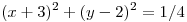 .
.
(b) Hallar las curvas planas tales que la recta normal en todo punto pasa por el origen
Punto V
Demuestre que el flujo de 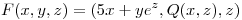 a traves del trozo de esfera de ecuación
a traves del trozo de esfera de ecuación 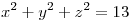 con
con  no depende de la funcion
no depende de la funcion 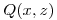 .
Indique gráficamente la orientación que ha elegido para el versor normal a la superficie y otras hipótesis que deberia considerar.
.
Indique gráficamente la orientación que ha elegido para el versor normal a la superficie y otras hipótesis que deberia considerar.
