Examen Final - 05/07/2007 - Tema 1
Cátedra: igual para todas
Fecha: 1º Oportunidad - (1º Cuatrimestre) 2007
Día: 05/07/2007
Enunciado
(1) Hallar el flujo de F a través de la superficie descripta por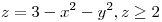 
con 
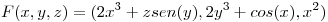. Mostrar la normal elegida.
(2) Hallar la circulación a través de la curva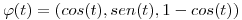 
si existe 
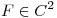con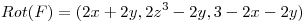 
(3) Hallar la masa del alambre que es intersección de 
y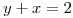 
en el primer octante si su densidad está dada por la distancia al plano 
.
(4) Responder a cada uno de los siguientes problemas, justificando brevemente su respuesta:
- Hallar la familia de curvas ortogonales a
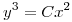. Encontrar la que pasa por el 
- Hallar la circulación de
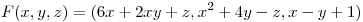a través de la curva 
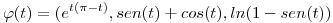con ![<tex>t\in[0,\pi]</tex>](lib/plugins/latex/images/117c3dc134d1bc388be9307bbfa6c5378b089a7f_0.png "<tex>t\in[0,\pi]</tex>")
.
(5) Plantear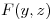 
y 
, funciones continuas pertenecientes a 
no constantes y 
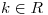tales que: el flujo de 
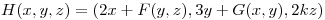a través del cuerpo encerrado por 
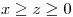y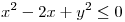 
sea igual al volumen del cuerpo.
(Los enunciados no son copia fiel de los que estaban en el final, pero los valores sí lo son. No nos acordamos de la redacción exacta)
Resolución
Punto I
La superficie descripta es un paraboloide hiperbolico que cae desde 
, para todos los puntos de 
.
Para no calcular el flujo a través de esa superficie del campo F, ya que quedaria una integral espantosa, planteo el teorema de gauss.
usando como cuerpo, el volumen que encierra el paraboloide(superficie sigma) y el plano Z=2(superficie sigma auxiliar).Para esto elijo la normal saliente del cuerpo, que es como lo calcula el teorema.
entonces tengo que:
.
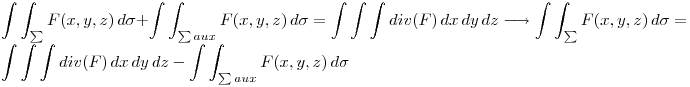Busco la integral triple de la divergencia:
Para el cuerpo planteado, en coordenadas cilindricas, si proyectamos sobre el plano xy veo que:
, 
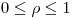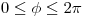y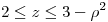 
.
A su ves Si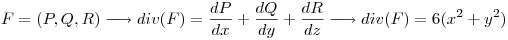 
que en coordenadas cilindricas lo escribo como 
.
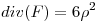Por lo tanto tengo que: ![<tex> \int\int\int div(F) \,dx\,dy\,dz = \int _{0}^{2 \pi } \int _{0}^{1} \int _{2}^{3-\rho^2} div(F) \rho \,dz \,d\rho \,d\phi = \int _{0}^{2 \pi } \int _{0}^{1} \int _{2}^{3-\rho^2} (6\rho^2) \rho \,dz \,d\rho \,d\phi = 12 \pi \int _{0}^{1} \int _{2}^{3-\rho^2} \rho^3 \,dz \,d\rho = 12\pi \int _{0}^{1} \rho^3(1-\rho^2) \,d\rho=12\pi \left[ \frac{\rho^4}{4} - \frac{\rho^6}{6} \right] _{0}^{1} = \pi</tex>](lib/plugins/latex/images/9038683230aa45ade111b464200c5a8c1574e887_0.png "<tex> \int\int\int div(F) \,dx\,dy\,dz = \int _{0}^{2 \pi } \int _{0}^{1} \int _{2}^{3-\rho^2} div(F) \rho \,dz \,d\rho \,d\phi = \int _{0}^{2 \pi } \int _{0}^{1} \int _{2}^{3-\rho^2} (6\rho^2) \rho \,dz \,d\rho \,d\phi = 12 \pi \int _{0}^{1} \int _{2}^{3-\rho^2} \rho^3 \,dz \,d\rho = 12\pi \int _{0}^{1} \rho^3(1-\rho^2) \,d\rho=12\pi \left[ \frac{\rho^4}{4} - \frac{\rho^6}{6} \right] _{0}^{1} = \pi</tex>")
.
Busco Flujo a través del plano 
, tomando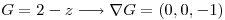 
que verifica la normal que deseamos.
Si proyecto mi superficie sobre el plano xy obtengo una circunferencia de radio 1 centrada en el origen.
Entonces tenemos que:
.
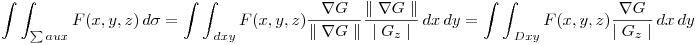Calculo: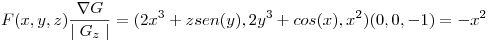 
Paso a coordenadas polares: 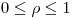y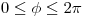
me queda que: ![<tex> \int \int_{ \, dxy } F(x,y,z) \frac{\nabla G}{ \mid G_{z} \mid }\,dx \,dy=\int_{0}^{1}\int_{0}^{2\pi}-\rho^2 cos^2(\phi)\rho\,d\sigma\,d\rho=- \left[ \frac{\rho^4}{4} \right]_{0}^{1} \left[ \frac{1}{2} + \frac{1}{4} \sin (2 \phi) \right]_{0}^{ 2 \pi }= -\frac{1}{4} \pi </tex>](lib/plugins/latex/images/641c9d0f4e0512f84bb8507c92f516cea31b2f27_0.png "<tex> \int \int_{ \, dxy } F(x,y,z) \frac{\nabla G}{ \mid G_{z} \mid }\,dx \,dy=\int_{0}^{1}\int_{0}^{2\pi}-\rho^2 cos^2(\phi)\rho\,d\sigma\,d\rho=- \left[ \frac{\rho^4}{4} \right]_{0}^{1} \left[ \frac{1}{2} + \frac{1}{4} \sin (2 \phi) \right]_{0}^{ 2 \pi }= -\frac{1}{4} \pi </tex>")
.
Por lo tanto: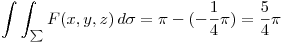
.
