Examen Final - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: 2da Oportunidad - 2do Cuatrimestre 2005
Día: 13/12/2005
Enunciado
- Sea
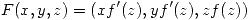 donde
donde 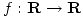
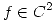 tal que
tal que  y
y  .
.
Calcular el flujo de a través de la superficie desripta por
a través de la superficie desripta por 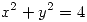 ,
,  , con la normal alejándose del eje
, con la normal alejándose del eje  .
. - Siendo

 . Calcular el flujo del rotor del campo
. Calcular el flujo del rotor del campo  a través de la semiesfera
a través de la semiesfera  ,
,  con la normal de cordenada
con la normal de cordenada  .
. - Sea
 . Hallar
. Hallar  de manera que el flujo de
de manera que el flujo de  a través de
a través de  ,
, 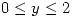 orientada de manera que su normal se aleje del eje
orientada de manera que su normal se aleje del eje  , sea
, sea  .
. - Responder a cada uno de los siguientes problemas, justificando brevemente su respuesta:
- Sea el campo
 . Hallar una esfera que contenga al origen de manera que el flujo de
. Hallar una esfera que contenga al origen de manera que el flujo de  hacia el exterior de la esfera no sea
hacia el exterior de la esfera no sea  .
. - Hallar
 para que la mínima distancia al origen de la curva de ecuación
para que la mínima distancia al origen de la curva de ecuación  sea
sea  .
.
- Hallar
 e
e  sabiendo que
sabiendo que  y que la recta tangente al gráfico de
y que la recta tangente al gráfico de  en
en  tiene ecuación
tiene ecuación  .
. - Hallar el volumen de la región del espacio descripta por
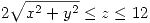 ,
,  .
.
Resolución
Punto I
La región a través de la cual se pretende calcular el flujo es un trozo de cilindro como el que muestra la figura:
Chimento: Cualquier intento de aplicar el teorema de Gauss (o Teorema de la Divergencia) nos va a fallar. Nos va a quedar una f(z) que nunca nos vamos a poder sacar de encima.
Aprovechando el chimento anterior, optamos por calcular ese flujo “manualmente”. Para ello, parametrizamos la superficie. Por tratarse de una figura cilíndrica muy “generosa” (es decir, está centrada en el origen y no da problemas), ni dudamos en parametrizar utilizando coordenadas cilíndricas. El resultado de la parametrización es el siguiente:
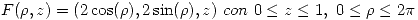
Entonces:


Con lo cual:

Es cuestión de hacer algunas pruebas con el resultado anterior, dándole valores a 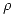 , para ver que el normal de esa superficie resulta saliente; es decir, se “aleja” del eje z, tal como pide el enunciado.
, para ver que el normal de esa superficie resulta saliente; es decir, se “aleja” del eje z, tal como pide el enunciado.
Ya podemos ir armando el “paquete” a integrar. Empezamos con la composición de la superficie con el campo vectorial:

Expresar el producto interno de esa composición con el normal de la superficie en la integral resulta en una expresión muy larga. Directamente ponemos la cuenta:

Operando:

Finalmente, con los límites de integración:
![<tex> 4 \cdot \int_0^{2 \pi} d \rho \int_0^1 f'(z) \cdot dz = 4 \cdot \int_0^{2 \pi} d \rho \cdot \Big[ f(z) \Big]_0^1 </tex> <tex> 4 \cdot \int_0^{2 \pi} d \rho \int_0^1 f'(z) \cdot dz = 4 \cdot \int_0^{2 \pi} d \rho \cdot \Big[ f(z) \Big]_0^1 </tex>](lib/plugins/latex/images/7450d6d4add74c9a2c16591f0fa4c599956260f2_0.png)
Usando los datos del enunciado:
![<tex> \Big[ f(z) \Big]_0^1 = f(1) \ - \ f(0) = 4 \ - \ (-1) = 5 </tex> <tex> \Big[ f(z) \Big]_0^1 = f(1) \ - \ f(0) = 4 \ - \ (-1) = 5 </tex>](lib/plugins/latex/images/292dd221d72e32446f147a05055387bbba60e963_0.png)
Con lo cual:


