Tabla de Contenidos
Examen Final - 61.03. Análisis Matemático II A
Cátedra: Todas
Fecha: Primera Oportunidad - Primer Cuatrimestre 2006
Día: 04/07/2006
Esta página está incompleta; podés ayudar completando el material.
Enunciado
(Los alumnos del primer cuatrimestre del 2005 deberán resolver los ejercicios 1,2,3,4,6, los restantes los ejercicios 1,2,3,4,5)
- Sea
 la región del espacio descripta por
la región del espacio descripta por  ,
,  ,
,  ,
, 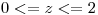 . Hallar
. Hallar  de manera que el flujo del campo
de manera que el flujo del campo  hacia el exterior de
hacia el exterior de  sea
sea  .
. - Dado
 hallar
hallar  y
y  de manera que
de manera que  , y calcular la circulación de
, y calcular la circulación de  a lo largo de la curva descripta por
a lo largo de la curva descripta por  ,
,  ,
,  , orientada de manera que la coordenada
, orientada de manera que la coordenada  de su tangente sea positiva.
de su tangente sea positiva. - Dado
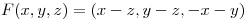 hallar la circulación de
hallar la circulación de  a lo largo del perímetro del cuadrilátero de vértices
a lo largo del perímetro del cuadrilátero de vértices  ,
,  ,
,  ,
,  , recorrido según el orden en que los puntos han sido dados.
, recorrido según el orden en que los puntos han sido dados. - Responder a cada uno de los siguientes problemas, justificando brevemente su respuesta:
- Sea
 una región de área 3 en el plano de ecuación
una región de área 3 en el plano de ecuación  . Hallar el flujo del campo
. Hallar el flujo del campo  a través de
a través de  , con el normal de coordenada
, con el normal de coordenada  positiva.
positiva. - Dada
 , hallar la circulación de
, hallar la circulación de  a lo largo de la curva parametrizada por
a lo largo de la curva parametrizada por  con
con  desde
desde  a
a 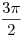 .
.
- Hallar una solución de la ecuación diferencial
 cuyo gráfico pase por el punto
cuyo gráfico pase por el punto  .
. - Sea
 la región de
la región de 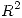 descripta por
descripta por 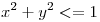 ,
,  ,
,  . Hallar el área de la superficie parametrizada por
. Hallar el área de la superficie parametrizada por  ,
,  .
.
Resolución
Discusión
Estás invitado a resolver este exámen.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
