Examen Final - 13/07/2004 - Tema 4
Enunciado
- Sea
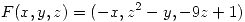 y sea
y sea  la curva borde de la superficie parametrizada por
la curva borde de la superficie parametrizada por 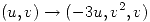 ,
, 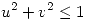 . Calcular la circulación de
. Calcular la circulación de 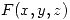 a lo largo de
a lo largo de  , orientada de tal manera de seguir el orden
, orientada de tal manera de seguir el orden 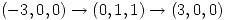 .
. - Sea, cuando
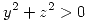 ,
, 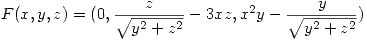 . Mostrar que el flujo de
. Mostrar que el flujo de  a través de la superficie descripta por
a través de la superficie descripta por 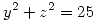 ,
, 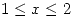 es igual al flujo de
es igual al flujo de  a través de la superficie descripta por
a través de la superficie descripta por 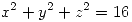 ,
, 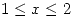 con la orientación elegida en ambos casos con la normal alejándose del eje
con la orientación elegida en ambos casos con la normal alejándose del eje  .
. - Dada la región
 descripta por
descripta por 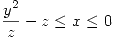 ,
, 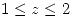 graficar aproximadamente
graficar aproximadamente  y calcular
y calcular 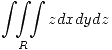 .
. - Responder a cada uno de los siguientes problemas, justificando brevemente su respuesta:
- Graficar aproximadamente la curva en
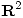 descripta en coordenadas polares por
descripta en coordenadas polares por 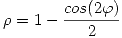 ,
, 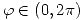 .
. - Hallar
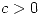 y
y 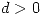 de manera que el área encerrada por la elipse de ecuación
de manera que el área encerrada por la elipse de ecuación 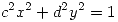 que pasa por
que pasa por 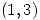 sea mínima. (Nota: el área encerrada por una elipse de ecuación
sea mínima. (Nota: el área encerrada por una elipse de ecuación 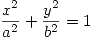 es
es 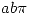 ).
).
- Hallar todos los puntos de intersección con la recta de ecuación
 de la línea de flujo que pasa por
de la línea de flujo que pasa por  del campo
del campo 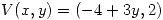 .
.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
