Examen Final 09/12/2003 - Tema 1
Enunciado
- Sea
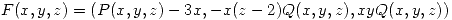 un campo vectorial
un campo vectorial  en la región
en la región 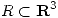 descripta por
descripta por 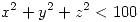 . Suponiendo que
. Suponiendo que 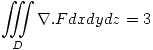 , siendo
, siendo  la región descripta por
la región descripta por 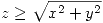 ,
, 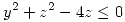 , calcular el flujo de
, calcular el flujo de  a través de
a través de  , siendo
, siendo  la superficie descripta por
la superficie descripta por 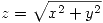 ,
, 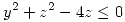 , orientada de manera que la componente
, orientada de manera que la componente  de su vector normal sea positiva.
de su vector normal sea positiva. - Sea
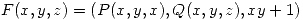 un campo vectorial
un campo vectorial 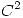 en la región
en la región  descripta por
descripta por 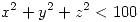 . Suponiendo que
. Suponiendo que 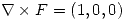 en
en  , calcular la circulación de
, calcular la circulación de  a lo largo de la curva en el plano
a lo largo de la curva en el plano  , parametrizada por
, parametrizada por 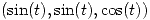 , con
, con  variando desde
variando desde  hasta
hasta  .
. - Sea
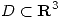 la región descripta por
la región descripta por  ,
, 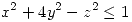 . Hallar el área de la proyección de
. Hallar el área de la proyección de  sobre el plano
sobre el plano 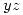 . Ilustrar graficamente.
. Ilustrar graficamente. - Responder a cada uno de los siguientes problemas, justificando brevemente su respuesta:
- Hallar una ecuación del plano tangente en
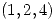 a la superficie de ecuación
a la superficie de ecuación 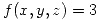 , sabiendo que la funcion
, sabiendo que la funcion 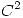
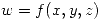 tiene, sujeta a la condición
tiene, sujeta a la condición 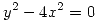 , máximo relativo
, máximo relativo 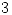 en
en 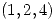 , y que
, y que 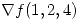 es no nulo.
es no nulo. - Calcular la circulación del campo
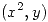 a lo largo de la curva definida por
a lo largo de la curva definida por 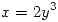 , desde
, desde  hasta
hasta 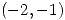 .
.
- Un corcho flota en la superficie de un río estacionario (es decir que la velocidad
 del fluído en cada punto
del fluído en cada punto  de la superficie depende de su posición
de la superficie depende de su posición  pero no del tiempo). El río fluye según el campo de velocidades
pero no del tiempo). El río fluye según el campo de velocidades  . Si el corcho pasa por el punto
. Si el corcho pasa por el punto  , ¿en qué punto cortará su trayectoria a la recta
, ¿en qué punto cortará su trayectoria a la recta  ?
?
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
