Paricalito - 28. Análisis Matemático I

Sede: Drago
Fecha: Primer Cuatrimestre 2004
Día: xx/xx/2004
Temas: Unidades 1 y 2

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Considere la función: $<tex>f(x) = 3 \cdot \sin (2x - \frac{\pi}{2}) + 1</tex>$
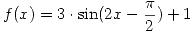
1. Graficar a partir de corrimientos
2. Indicar período, amplitud e Im(f)
Ahora pensemos en esta otra función: 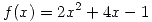$<tex>f(x) = 2x^2 + 4x - 1</tex>$ con $<tex>f:(- \infty,-1] \rightarrow [-3,+ \infty)</tex>$
1. Graficar. ¿Es f(x) biyectiva? Definir 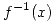$<tex>f^{-1}(x)</tex>$ (fórmula, dominio, codominio)
2. Consideremos la Imf: ¿Tiene cotas superiores? ¿Cuál es el supremo? ¿Tiene cotas inferiores? ¿Cuál es el ínfimo?
Para los valientes:
Sea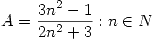 $<tex>A = { \frac{3n^2 - 1}{2n^2 +3} : n \in N}</tex>$ .
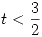1. Demuestre que $<tex>\frac{3}{2}</tex>$ es el supremo del conjunto (Pista: primero verificar que es cota superior. Después ver que no hay ningún $<tex>t < \frac{3}{2}</tex>$ que pueda ser cota superior).
2. ¿Tiene este conjunto cotas inferiores? ¿Cuál es el ínifimo?

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.