Examen Parcial - 76.01. Introducción a la Ingeniería Química I
- Enunciado
  - Punto I
  - Punto II
- Resolución
  - Punto I
  - Punto II
- Discusión

Examen Parcial - 76.01. Introducción a la Ingeniería Química I

Cátedra: Campanella
Fecha: Primera Oportunidad - Primer Cuatrimestre 2006
Día: 30/05/2006

En la figura se muestra el esquema de la instalación disponible en una planta de procesamiento petroquímico. Dicha instalación incluye un intercambiador de calor y un separador bifásico. El intercambiador de calor emplea agua a presión atmosférica como fluído refrigerante. El agua ingresa a la cañería a 25ºC, con una velocidad promedio de $<tex>1.5 m/seg</tex>$ , y egresa como vapor saturado.

Actualmente, se está pensando en emplear dicha instalación para procesar una mezcla gaseosa de hidrocarburos a fin de obtener una corriente líquida en el separador (L), con una concentración molar de butano superior al 60%.

Decida si es posible emplear esta instalación para tal fin. Justifique su respuesta.
Por otro lado, se está considerando la posibilidad de emplear la corriente de hidrocarburos de salida del intercambiador para precalentar otra corriente de la planta. De implementarse esta alternativa, la temperatura de la corriente de hidrocarbuos al final de la cañería (antes del separador) disminuiría hasta 114ºC. Además, en estas condiciones la concentración molar de etano en el vapor (V) sería del 36.4%.

¿Es posible emplear la instalación en estas condiciones? Justifique su respuesta.

Datos de la alimentación
$<tex>Z_{C2}^1=0.2; \quad Z_{C3}^1=0.2; \quad Z_{C4}^1=0.6; \quad F_1=480\,\mbox{kmol/h}; \\ T_1=873\,K; \quad P_1=40\,atm</tex>$

Cañería de agua: 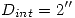$<tex>D_{int}=2''</tex>$

Entalpía de la mezcla puede aproximarse con la función:
$<tex>h=18345-9.1634\cdot T+0.1557\cdot T^2 -5\cdot 10^{-5}\cdot T^3 \quad \ h [kj/kmol], T[K]</tex>$

Punto II

Debido al creciente desarrollo de la industria farmacológica una PYME decide incursionar en el mercado a través de la venta de gases de esterilización. Para ello se realizó un estudio de mercado previo y un análisis sobre la tecnología del proceso.

Los estudios arrojaron los siguientes datos:

El óxido de etileno ( $<tex>C_2H_4O</tex>$ ) es el gas más utilizado en la industria,
En general el llenado de gases se realiza en forma adiabático o isotérmica de acuerdo a las normativas que regulan este tipo de actividad.
Se comercializa en ampollas, cartuchos, films y esterilizadores.

Normativas del almacenamiento:

El óxido se almacena en estado líquido, bien como líquido refrigerado o bien como gas comprimido licuado a temperatura ambiente, pero siempre bajo presión de gas inerte ( $<tex>N_2</tex>$ ).
Si se almacena con $<tex>N_2</tex>$ la presión del sistema deberá mantenerse dentro de la zona de segurida detallada en el gráfico 1.
En ningún caso el llenado máximo del recipiente superará $<tex>0.78Kg</tex>$ de óxido de etileno por $<tex>dm^3</tex>$ .
Por encima de los 212ºF el óxido se polimeriza generando obstrucciones en válvulas, filtros y puntos muertos del sistema.

En base a estos conceptos se decidió comenzar con la venta de cartuchos de $<tex>5dm^3</tex>$ de capacidad. Para esta producción se dispone de lineas de llenado con óxido de etileno prácticamente puro ( $<tex>7 Kg/cm^2\mbox{ y }323K</tex>$ ). Los envases contendrán inicialmente $<tex>N_2</tex>$ puro a $<tex>1 atm\mbox{ y }303K</tex>$ .

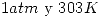Determine el procedimiento de llenado correcto para este proceso, justificando su respuesta. (Considere comportamiento ideal de los gases en todo el desarrollo).

Capacidades caloríficas calculadas para el proceso:

T	Cp
303 K	11.70 cal/gmolºC
323 K	12.25 cal/gmolºC
333 K	12.75 cal/gmolºC

Resolución

Punto I

Parte a

Comenzaremos calculando el flujo de agua en el serpentín del intercambiador:
$<tex>\dot{M}_e^{H_2O}=\rho_e\cdot v_e\cdot A_e=\rho_{H_2O(l)}\cdot v_e\pi\frac{D^2}{4}=1\frac{g}{cm^3}150\frac{cm}{seg}\pi\frac{(5,08cm)^2}{4}=3040\frac{g}{seg}</tex>$
donde la densidad del agua líquida la hemos supuesto constante por consideraciones de líquido incompresible.

$<tex>\dot{N}_e^{H_2O}=3040\frac{g}{seg}\frac{1gmol}{18g}\frac{60seg}{1min}\frac{60min}{1hora}=608\frac{kmol}{h}</tex>$

Luego si planteamos el balance de materia para un volumen de control de agua dentro del serpentín, y consideramos que el régimen es estacionario:
$<tex>\mbox{B.M.}H_2O \quad \dot{N}_e^{H_2O}-\dot{N}_s^{H_2O}=\left.\frac{dN}{d\theta}\right|_{VC}=0 \quad \Rightarrow \quad \dot{N}_e^{H_2O}=\dot{N}_s^{H_2O}</tex>$

Ahora cómo nuestro principal objetivo es hallar la temperatura de la mezcla de hidrocarburos a la salida del intercambiador, trataremos de hallar el calor intercambiado entre ambos fluidos, y despreciando las pérdidas de calor con el ambiente, ambos calores serán iguales (en módulo).

$<tex>\mbox{B.E.}H_2O \quad \dot{Q}_{H_2O}=\dot{N}_{H_2O}[\lambda_{vap}^{373K}+C(373K-298K)]</tex>$

Buscando los valores en las tablas (y considerando que $<tex>C</tex>$ es constante): $<tex>\lambda_{vap}^{373K}=9717\frac{cal}{gmol} \quad C=1\frac{cal}{g\cdot K}\frac{18g}{gmol}</tex>$ . Entonces:

$<tex>\dot{Q}_{H_2O}=6.729\cdot 10^{9}\frac{cal}{h}</tex>$

Ahora lo hacemos para la mezcla:

$<tex>\mbox{B.E.mezcla} \quad \dot{F}(h_e-h_s)+\dot{Q}_s=\left.\frac{dE}{d\theta}\right|_{VC}=0</tex>$

El término 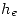$<tex>h_e</tex>$ se evalúa usando la ecuación dato en $<tex>T=873K</tex>$ , resultando:
$<tex>h_e=95741.9\frac{kJ}{kmol}\cdot\frac{2kcal}{8.31kJ}=23042.6\frac{kcal}{kmol}</tex>$

Recordando que (del enunciado): $<tex>\dot{F}=480\frac{kmol}{h}</tex>$ , y que además: $<tex>\dot{Q}_{s}=\dot{Q}_{H_2O}</tex>$ ; resolvemos el balance:

$<tex>h_s=h_e+\frac{\dot{Q}_s}{\dot{F}}=9021.76\frac{kcal}{kmol}\frac{8.31kJ}{2kcal} =37485.44\frac{kJ}{kmol}</tex>$
$<tex>0=-19140.44-9.1634\cdot T_s+0.1557\cdot T_s^2 -5\cdot 10^{-5}\cdot T_s^3</tex>$

Resolviendo esta ecuación mediante iteraciones (o alguna calculadora especial), podemos hallar que $<tex>T_s=411.8K</tex>$

A esta temperatura debemos preguntarnos en que fase estará la mezcla, entonces vamos a suponer que está en el punto de rocío. Esto se traduce en que la composición de la mezcla es igual a la composición del vapor, es decir que: $<tex>y_{C2}=0.2 \quad y_{C3}=0.2 \quad y_{C4}=0.6</tex>$

Para buscar en los nomogramas de L'eprestier, debemos tener los datos en unidades USCS, estos son: $<tex>P=40atm=587.84psi</tex>$ y $<tex>T=411.8K=281.84F</tex>$ . Obtenemos del nomograma entonces:
$<tex>K_{C2}=3.4 \quad K_{C3}=1.8 \quad K_{C4}=0.88</tex>$

Ahora si estuviese en punto de rocío debería cumplirse que $<tex>x_{C2}+x_{C3}+x_{C4}=1</tex>$ , pero observamos que $<tex>x_{C2}+x_{C3}+x_{C4}=\frac{y_{C2}}{K_{C2}}+\frac{y_{C3}}{K_{C3}}+\frac{y_{C4}}{K_{C4}}=0.851<1</tex>$ , lo que significa que en el punto de rocío las constantes deben ser menores, lo que se obtendría con una temperatura menor, por lo tanto $<tex>T_s>T_{rocio}</tex>$ y la mezcla es todo gaseosa y la planta no se podrá utilizar para obtener butano líquido.

Parte b

Ahora vamos a suponer que la mezcla entra al tanque flash con una temperatura de 114ºC, es decir $<tex>T=237.2F</tex>$ , entonces con este dato podemos hallar las constantes de equilibrio líquido-vapor en los nomogramas:
$<tex>K_{C2}=2.75 \quad K_{C3}=1.35 \quad K_{C4}=0.62</tex>$

Escribiendo los balanaces de masa:

$<tex>\mathbf{Global: } \quad \dot{F}=\dot{V}+\dot{L}</tex>$

$<tex>\mathbf{Etano: } \quad z_{C2}\dot{F}=y_{C2}\dot{V}+x_{C2}\dot{L}</tex>$

$<tex>\mathbf{Butano: } \quad z_{C4}\dot{F}=y_{C4}\dot{V}+x_{C4}\dot{L}</tex>$

En el segundo podemos reemplazar $<tex>L</tex>$ por $<tex>F-V</tex>$ , y $<tex>x_{C2}=\frac{y_{C2}}{K_{C2}}</tex>$ , pues $<tex>y_{C2}</tex>$ es dato de enunciado. Despejamos entonces:
$<tex>\left( z_{C2}-\frac{y_{C2}}{K_{C2}} \right)\cdot\dot{F}=\left( y_{C2}-\frac{y_{C2}}{K_{C2}} \right)\cdot\dot{V}</tex>$
de donde despejamos $<tex>\dot{V}=140.1\frac{kmol}{h}</tex>$ . Reemplazamos en el global para obtener $<tex>\dot{L}=339.9\frac{kmol}{h}</tex>$ .

Ahora en el de butano reemplazamos $<tex>y_{C4}=K_{C4}\cdot x_{C4}</tex>$ y despejamos la concentración de butano en el líquido: $<tex>x_{C4}=0.67</tex>$ . Por lo tanto se obtiene un 67% de butano en el líquido.

Punto II

Vamos a resolver el problema en 2 casos: adiabático e isotérmico. Luego veremos cuál es conveniente

Caso adiabático

Antes que nada debemos observar que los cartuchos se cargarán hasta que la presión alcance la presión de linea, entonces:
$<tex>N_0=\frac{P_0V}{RT_0}=\frac{1\cdot 5}{0.082\cdot 303}gmol=0.2012gmol</tex>$
$<tex>N_f=\frac{P_fV}{RT_f}=\frac{412.8gmol\cdot K}{T_f}</tex>$

Planteamos los balances:
$<tex>\mbox{Balance de masa:} \quad \frac{dN}{d\theta}=\dot{n}_e</tex>$
$<tex>\begin{array}{lrcl}\mbox{Balance de energ\'ia:} \quad & \displaystyle\frac{dE}{d\theta} & = & \dot{n}_e\cdot h_e \\ & \displaystyle\frac{dNu}{d\theta} & = & \displaystyle\frac{dN}{d\theta}h_e \\ & \displaystyle\int_{N_0u_0}^{N_fu_f}\!dNu & = & \displaystyle\int_{N_0}^{N_f}\!h_edN \\ & N_fu_f-N_0u_0 & = & (N_f-N_0)h_e \end{array}</tex>$

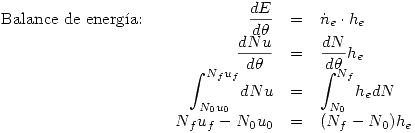
Para evaluar estas propiedades usaremos el estado de referencia en $<tex>T_{ref}=0K</tex>$ , por lo que evaluaremos:

$<tex>h_e=c_{p(T_e)}\cdot T_e=12.23\frac{cal}{gmol\cdot K}\cdot323K=3956.75\frac{cal}{gmol}</tex>$

$<tex>N_0u_0=N_0c_{V(T_0)}T_0=N_0(c_{P(T_0)}-R)T_0=N_0\cdot 2939.1\frac{cal}{gmol}=591.3cal</tex>$

$<tex>N_fu_f=N_fc_{V(T_f)}T_f=412.8gmolK\cdot C_{V(T_f)}</tex>$

Entonces:
$<tex>412.8gmolK\cdot c_{V(T_f)}-591.3cal=\left(\frac{412.8gmolK}{T_f}-0.2012gmol\right)\cdot3956.75\frac{cal}{gmol}</tex>$

$<tex>412.8gmolK\cdot(c_{P(T_f)}-2)+204.79=\frac{1.633\cdot 10^6}{T_f}</tex>$

Esto debería resolverse iterando, pero como todas las iteraciones las haremos extrapolando los datos de $<tex>c_p</tex>$ de la tabla para valores mayores utilizando los datos a 323 y 333K, entonces podemos hallar la relación entre estas variables mediante la función de extrapolación lineal:
$<tex>c_p(T_f)=\frac{12.75-12.25}{333-323}(T_f-333)+12.75</tex>$
$<tex>c_p(T_f)=0.05T_f-3.9</tex>$

Ahora reemplazamos en la ecuación:
$<tex>\begin{array}{ccccccccc} & & 412.8(0.05T_f & - & 3.9-2) & + & 204.79 & = & \frac{1.633\cdot 10^6}{T_f} \\ & & 20.64T_f & - & 2435.52 & + & 204.79 & = & \frac{1.633\cdot 10^6}{T_f} \\ & & 20.64T_f & - & 2230.73 & = & \frac{1.633\cdot 10^6}{T_f} & \\0 & = & 20.64T_f^2 & - & 2230.73T_f & - & 1.633\cdot 10^6 & \end{array}</tex>$

Esta ecuación tiene dos soluciones (donde una solución es negativa y descartaremos), por lo tanto $<tex>T_f=340.46K=67.46C</tex>$ .

Observamos que este valor cae fuera de la zona de seguridad. Por lo tanto no podrá usarse el llenado adiabático.

Caso Isotérmico

$<tex>P_f=P_L=6.77atm=685.9kPa</tex>$
$<tex>T_f=T_0=303K=30C</tex>$

Estos datos caen dentro de la zona de seguridad. Ahora verificaremos las demás condiciones de seguridad.

Como $<tex>T=86F</tex>$ entonces el óxido no se polimeriza.
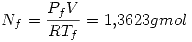$<tex>N_f=\frac{P_fV}{RT_f}=1.3623gmol</tex>$ que teniendo en cuenta los moles iniciales de nitrógeno, entonces al final hay $<tex>1.1612gmolC_2H_4O=51.155gC_2H_4O</tex>$ por lo que no supera el máximo de carga.

Entonces puede utilizarse el llenado isotérmico y no el adiabático.

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o mandáme un mail GK