75.23 - Inteligencia Artificial
Preguntas Varias de Parcial
- Complejidad computacional del Hill Climbing
- En
 es lineal
es lineal  se guarda la base de la última ramificación.
se guarda la base de la última ramificación.
- Complejidad computacional del A*
- Si
 es lineal
es lineal - Si no,
 ,
, 
- Si se aplica backtracking iterativo haciendo hasta el nivel N y si no se encuentra la solución se incrementa en 1 el nivel y se repite desde el principio y asi sucesivamente. ¿Es admisible? ¿Es optimal? ¿Por qué?
- Es admisible porque si existe la solución la encuentra ya que va incrementando los niveles. No es optimal porque para al encontrar la primera solución, no la mejor.
- ¿Por qué en IA no se calcula el árbol implícito aplicando todas las combinaciones y luego se utiliza la investigación operativa para buscar los caminos?
- Ocupa mucha memoria.
- Lleva mucho tiempo.
- Si el árbol fuese infinito se agotarían los recursos antes de comenzar a buscar la solución.
- ¿Qué es un sistema experto y cuáles son sus funciones?
- Un sistema experto es aquel que resuelve los problemas como lo haría un especialista o sea que utiliza la idea de igual razonamiento que el especialista. Sus funciones son:
- Entender la consulta
- Pedir datos
- Explicaciones (Why) justificación del pedido de datos
- Resolver el problema
- Sintetizar respuesta
- Explicar cómo se llegó al resultado
- ¿Cómo se implementa la función de explicación?
- Para explicar debe representar lo que va haciendo o sea debe marcar las clausulas que usa. Utiliza un programa prolog que funciona como compilador de prolog (Meta-intérprete). Representa internamente las reglas como datos. Por ende explica como llegó al goal.
- En el método A* se exige que los costos sean infinitésimos , ¿Por qué?
- Para que crezcan, y no se hagan tan pequeños, que se puedan ir por las ramas.
- En A*,

 costo de la ruta que va del nodo de partida al nodo n.
costo de la ruta que va del nodo de partida al nodo n. costo estimado de la ruta más barata que va de n a la meta.
costo estimado de la ruta más barata que va de n a la meta.
- Si se toma
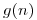 idénticamente nulo (
idénticamente nulo ( ). ¿Sigue siendo admisible?
). ¿Sigue siendo admisible?- Tenemos entonces que
 . Si tenemos
. Si tenemos 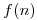 es igual al costo que me falta para llegar a la meta, el método se convertiría en deep first, ya que siempre se elegirían las ramas de menor costo, que son las más profundas, por lo tanto no es admisible ni optimal ya que no se puede encontrar la solución si existe, y si la encuentro, no puede garantizar que sea la óptima.
es igual al costo que me falta para llegar a la meta, el método se convertiría en deep first, ya que siempre se elegirían las ramas de menor costo, que son las más profundas, por lo tanto no es admisible ni optimal ya que no se puede encontrar la solución si existe, y si la encuentro, no puede garantizar que sea la óptima.
- Si hago
 , ¿Es admisible?, ¿Es optimal?
, ¿Es admisible?, ¿Es optimal?- Tenemos entonces que
 . Si la función de costo tomoa el costo existente desde el inicio al nodo n, siempre elegiría las de menor, que en este caso son las menos profundas, por lo que el método se convertiría en breath first. Este método, si hay solución la encuentra, por lo que es admisible, pero no optimal.
. Si la función de costo tomoa el costo existente desde el inicio al nodo n, siempre elegiría las de menor, que en este caso son las menos profundas, por lo que el método se convertiría en breath first. Este método, si hay solución la encuentra, por lo que es admisible, pero no optimal.
- Si se aplica bactracking hasta nivel n, se guardan bases hasta nivel n, luego para esa lista de bases se aplica A*. ¿Es admisible?, ¿Para qué se guardan las bases del nivel n?
- Encuentro la solución si o si , hasta el nivel n estoy realizando un backtracking iterativo, no encuentro la solución en el nivel 1 entonces subo el nivel y repito de nuevo, entonces es admisible pero ineficiente.