Examen Parcial - 75.12. Análisis Numérico

Cátedra: Menéndez-Tarela-Cavaliere
Fecha: Tercera Oportunidad - Segundo Cuatrimestre 2011
Día: 07/12/2011

Con los siguientes datos:

  ^ Datos          ^^^^^^^^^^^    
  | x | 4 | 4.2 | 4.5 | 4.7 | 5.1 | 5.5 | 5.9 | 6.3 | 6.8 | 7.1 |
  | y | 102.56 | 113.18 | 130.11 | 142.05 | 167.53 | 195.14 | 224.87 | 256.73 | 229.5 | 326.72 |

1. Construir la aproximación de mínimos cuadrados de la forma
2. Construir la aproximación de mínimos cuadrados de la forma
3. Determinar cuantitativamente cual de las dos alternativas ajusta mejor los datos de la tabla.

Se desea encontrar el cero de la función . Para ello se utilizará un método de punto fijo basado en la aplicación de la función generadora

1. Estudie las propiedades de convergencia del método propuesto. Encuentre explícitamente un intervalo de convergencia.
2. Tomando como valor de arranque encuentre el cero buscado con una tolerancia para el error relativo del 1%.
3. Estime el orden de convergencia del método.
4. Escriba un programa computacional ad-hoc para hallar el cero de esta función. Incluya la programación de la salida del cálculo en un archivo de datos.

AYUDA: el cero buscado está entre 0 y 1.

Ud. dispone de un programa ejecutable para calcular áreas en un intervalo a elección debajo de la curva de distribución normal de Gauss, , donde 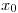y </tex>\sigma</tex> son el centro y la desviación estándar de la campana de Gauss. Indique cómo procede para determinar el error involucrado en el cálculo de un área determinada.

Para resolver un sistema de ecuaciones algebraicas no lineales se emplea un método de cuasi-Newton, consiste en congelar la matriz Jacobiana durante tres iteraciones suesivas, antes de volver a actualizarla. Explique en qué se gana y en qué se pierde velocidad de convergencia (obviamente, lo adecuado del método dependerá de si se gana más de lo que se pierde).