Examen Parcial - 75.03. Organización del Computador

Cátedra: Saubidet
Fecha: Primera Oportunidad - Segundo Cuatrimestre 2005
Día: 26/10/2005

Abacus: [ 5 ptos. ]

Se tiene una lista (L) cuya dirección de inicio se encuentra almacenada en la celda 200. Los nodos de la lista (L) representan los distintos concesionarios de una marca de autos. Cada nodo está formado por cuatro celdas contiguas en memoria:

1. La primera celda contiene un número que identifica al concesionario.
2. La segunda celda contiene la cantidad de autos en stock (sin vender) que tiene la concesionaria en ese momento.
3. La tercera celda contiene la cantidad de autos vendidos durante el mes hasta ese momento.
4. La cuarta celda contiene la dirección del siguiente nodo de la lista. El final de la lista (L) se indica con un valor -1 en la cuarta celda del último nodo.

Por otro lado se tiene un vector (V) que comienza en la celda 400 y que contiene elementos formados por tres celdas contiguas en memoria que representan novedades de ventas de vehículos o entregas de nuevos vehículos de la fábrica a los concesionarios. La primera celda de cada elemento del vector contiene el número de concesionario, la segunda celda contiene un O si es una venta o un 1 si es un auto nuevo entregado por la fábrica, y la tercera celda contiene la cantidad de vehículos asociados a la novedad. El final del vector se representa con un -1.

Se pide realizar un programa ABACUS con punto de carga en la celda 300 que recorra el vector (V) y actualice las unidades en stock y vendidas de cada concesionario, teniendo en cuenta que tanto la lista (L) como el vector (V) están ordenados por número de concesionario. Además se debe dejar en la celda 500 el número de concesionario que más autos vendió durante el mes.

Datos de la máquina: L(RPI) = 12 bits; L(CO) = 4 bits.

Códigos de operación:
0 - Carga Inmediata
1 - Carga
2 - Almacenar
3 - Suma
6 - Not (Ac)
7 - Bifurcación si (Ac) = 0
8 - Bifurcación si (Ac) > 0
9 - Bifurcación si (Ac) < 0
F - Fin de programa

Sistemas Numéricos: [2,5 ptos.]

Se dispone de un formato de representación de números flotantes en el cual se utilizan 3 bytes para almacenar el signo (1 bit) y la caracteristica como BPF s/signo (23 bits) y 4 bytes para almacenar los dígitos de la mantisa normalizados en base 16.

Se pide:

1. Indicar los números máximos y mínimos almacenables en este formato. (extremos de la escala de representación) [1 pto.]
2. Dado A = 7639613 que representa la configuración decimal de un número almacenado en formato empaquetado de 3 bytes, almacenar dicho número en el formato flotante propuesto indicando su configuración hexadecimal. [1,5 ptos.]

Sistemas Numéricos: [2,5 ptos.]

Dado A que representa la configuración en base 8 de un número almacenado en formato BPF c/signo de 16 bits y B que representa la configuración en base 16 de otro número almacenado en formato zoneado de 3 bytes se pide:

A=4646
B=F4F7D0

Se pide:

1. Indicar cuales son los números almacenados en base 10. [0,5 ptos.]
2. Restar ambos números (A - B) en formato BPF c/signo de 16 bits indicando la validez del resultado. [1,5 ptos.]
3. Si es posible, expresar el resultado de la resta anterior en formato BPFlotante de precisión simple dando su configuración decimal. [0,5 ptos.]

IMPORTANTE: Para aprobar el parcial es necesario tener correctamente resuelto el 60% del mismo y como mínimo 40% de cada tema. (Abacus y Numéricos) Las respuestas que no estén justifIcadas o estén mal justificadas se considerarán erróneas. Por favor, lea bien el enunciado.

1. Máximo positivo:
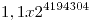
   Máximo negativo: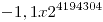
   Mínimo positvo: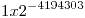
   Mínimo negativo: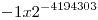

 11000000000000000000111100100100101010110000000000000000 

1. A = -3674 (base 10)
   B = -470 (base 10)
2. A - B = 1111001101111100 (base 2). El resultado es válido.

 11000101010010000100000000000000