Primer Parcial (Segundo Recuperatorio)- 62.15 Física III D
Cátedra: Arcondo
Fecha: Primer Parcial (Segundo Recuperatorio) - 1° Cuatrimestre
Día: 01/07/2008
Enunciado
Punto I
- Calcular la longitud de onda máxima de la luz que hará funcionar una celda fotoeléctrica dotada de un cátodo de tungsteno sabiendo que los fotoelectrones poseen una energía cinética máxima de 5,5 eV cuando son arrancados por una luz de
 Å.
Å. - Si esta radiación de
 Å e intensidad
Å e intensidad  incide sobre la celda fotoeléctrica (de área igual a
incide sobre la celda fotoeléctrica (de área igual a  ), siendo el rendimiento fotoeléctrico del 20 % (
), siendo el rendimiento fotoeléctrico del 20 % (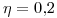 ). ¿Cuál sería la intensidad de la corriente eléctrica producida?
). ¿Cuál sería la intensidad de la corriente eléctrica producida?
Punto II
La serie de Humphreys del espectro del átomo de hidrógeno empieza a 12368 nm y se ha seguido hasta 3281,4 nm.
- ¿Qué tipo de transiciones están implicadas? (¿De que nivel inicial a que nivel final?)
- Obtenga la expresión que indica cuáles son los valores de longitud de onda de las transiciones intermedias.
Punto III
Si la incertidumbre en la energía de un estado excitado de un sistema es de 1,1 eV.
- ¿Cuál es el promedio de la duración en ese estado?
- Si el nivel de energía de dicho estado fuera de 1,6 KeV, ¿cuál será la mínima incertidumbre en la longitud de onda del fotón emitido cuando el estado excitado decaiga al nivel fundamental? (Durante el parcial se aclaró que 1,6 KeV era la energía necesaria para llevarlo del estado fundamental al excitado)
Punto IV
- Indicar los valores de
 de las líneas espectrales que se observan en la transición
de las líneas espectrales que se observan en la transición 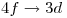 .
. - Si se aplica un campo magnético de 0,5 T, ¿serán diferenciables las líneas en un espectómetro de resolución
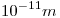 ?
? - Determinar los momentos magnéticos posibles en el nivel energético
 . ¿Qué predice la teoría de Bohr?
. ¿Qué predice la teoría de Bohr?
Resolución
Punto I
- Calcular la longitud de onda máxima de la luz que hará funcionar una celda fotoeléctrica dotada de un cátodo de tungsteno sabiendo que los fotoelectrones poseen una energía cinética máxima de 5,5 eV cuando son arrancados por una luz de
 Å.
Å. - Si esta radiación de
 Å e intensidad
Å e intensidad  incide sobre la celda fotoeléctrica (de área igual a
incide sobre la celda fotoeléctrica (de área igual a  ), siendo el rendimiento fotoeléctrico del 20 % (
), siendo el rendimiento fotoeléctrico del 20 % (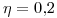 ). ¿Cuál sería la intensidad de la corriente eléctrica producida?
). ¿Cuál sería la intensidad de la corriente eléctrica producida?
Primero podemos calcular cual es la función de trabajo del cátodo de tungsteno:
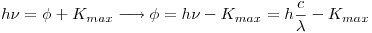
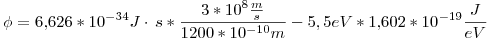
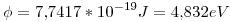
Cuando incide un fotón con mínima energía para hacer funcionar una celda fotoeléctrica, tenemos que la energía cinética máxima es 0:
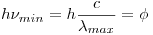
Despejando  queda:
queda:

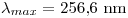
Si se toma un  mayor a 256.6 nm, la frecuencia
mayor a 256.6 nm, la frecuencia 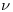 será menor, y por lo tanto, su energía
será menor, y por lo tanto, su energía 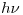 también será menor y no será suficiente para producir efecto fotoeléctrico (porque es menor que
también será menor y no será suficiente para producir efecto fotoeléctrico (porque es menor que  ).
).
Para el próximo punto, sabemos que un fotón con  Å tiene una energía
Å tiene una energía 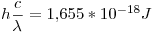 . Por lo tanto, para tener una potencia de
. Por lo tanto, para tener una potencia de  necesitaremos
necesitaremos 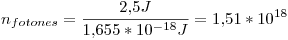 fotones por segundo por
fotones por segundo por 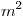
Como el área de la celda fotoeléctrica es de  (
( ), la cantidad de fotones incidentes serán:
), la cantidad de fotones incidentes serán:
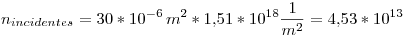 fotones por segundo.
fotones por segundo.
El rendimiento fotoeléctrico es 0.2 quiere decir que no todos los fotones incidentes consiguen arrancar electrones que contribuyan a la corriente electrica. Como lo que nos interesa saber es cuanto electrones aportan a la corriente eléctrica, calculamos:
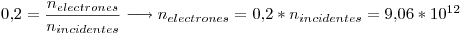
Por lo tanto tenemos que 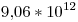 electrones son arrancados por segundo y contribuyen a la corriente eléctrica.
Entonces, la intensidad de la corriente eléctrica (carga/segundo) será:
electrones son arrancados por segundo y contribuyen a la corriente eléctrica.
Entonces, la intensidad de la corriente eléctrica (carga/segundo) será:
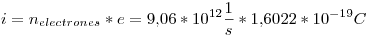
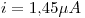
Punto II
La serie de Humphreys del espectro del átomo de hidrógeno empieza a 12368 nm y se ha seguido hasta 3281,4 nm.
- ¿Qué tipo de transiciones están implicadas? (¿De que nivel inicial a que nivel final?)
- Obtenga la expresión que indica cuáles son los valores de longitud de onda de las transiciones intermedias.
Para el hidrógeno tenemos que:
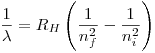
Si tomamos  , la segunda parte de la igualdad es máxima, es decir, la diferencia
, la segunda parte de la igualdad es máxima, es decir, la diferencia 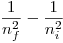 es máxima. Para hacer esa diferencia máxima, podemos decir que
es máxima. Para hacer esa diferencia máxima, podemos decir que 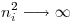 , y siendo que n es entero,
, y siendo que n es entero, 
Por lo tanto:
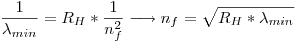
La menor longitud de onda observada es 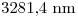 , entonces:
, entonces:
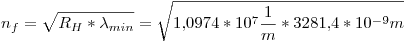
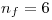
Por otro lado, si  es máximo, la diferencia
es máximo, la diferencia 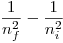 es mínima. Siendo que
es mínima. Siendo que 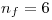 , para que la diferencia sea mínima tenemos que tomar
, para que la diferencia sea mínima tenemos que tomar 
Por lo tanto:
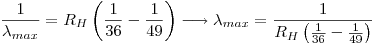
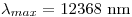 , que es el resultado que esperabamos encontrar por enunciado.
, que es el resultado que esperabamos encontrar por enunciado.
Sabiendo cual es  , la expresión para las longitudes de onda intermedias es fácil de encontrar:
, la expresión para las longitudes de onda intermedias es fácil de encontrar:
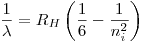
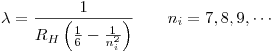
Punto III
Si la incertidumbre en la energía de un estado excitado de un sistema es de 1,1 eV.
- ¿Cuál es el promedio de la duración en ese estado?
- Si el nivel de energía de dicho estado fuera de 1,6 KeV, ¿cuál será la mínima incertidumbre en la longitud de onda del fotón emitido cuando el estado excitado decaiga al nivel fundamental? (Durante el parcial se aclaró que 1,6 KeV era la energía necesaria para llevarlo del estado fundamental al excitado)
Del principio de incertidumbre:
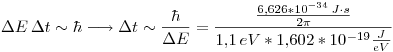
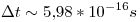
Lo que sigue no estoy seguro que esté bien
Primero, calculamos el valor de  :
:
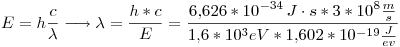
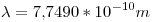
Ahora calculamos la incertidumbre:
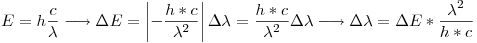
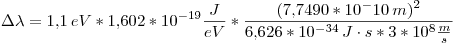
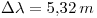
Punto IV
- Indicar los valores de
 de las líneas espectrales que se observan en la transición
de las líneas espectrales que se observan en la transición 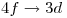 .
. - Si se aplica un campo magnético de 0,5 T, ¿serán diferenciables las líneas en un espectómetro de resolución
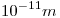 ?
? - Determinar los momentos magnéticos posibles en el nivel energético
 . ¿Qué predice la teoría de Bohr?
. ¿Qué predice la teoría de Bohr?
Para el primer punto, siendo que no nos dicen que hay algún campo magnético, solo nos importa  y
y  .
.
En ese caso, 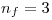 y
y 
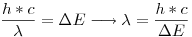
Sabemos que 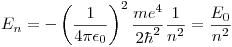 para el hidrógeno.
para el hidrógeno.
En este caso, tenemos que
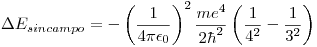

Reemplazando en la ecuación anterior:
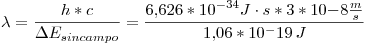
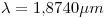
Si se aplica un campo magnético de 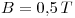 , la energía de un estado depende de
, la energía de un estado depende de 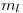 y
y 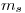 :
:
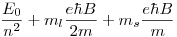
Entonces, al igual que antes:
\lambda = \frac{h*c}{\Delta E}
Solo que al aplicar un campo magnético, la energía depende de 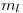 y
y 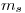 .
.
![<tex>\Delta E = E_f - E_i = \left[-\frac{E_0}{3^2} +m_{l_f}\frac{e \hbar B}{2 m} + m_{s_f}\frac{e \hbar B}{m}\right] - \left[-\frac{E_0}{4^2} +m_{l_i}\frac{e \hbar B}{2 m} + m_{s_i}\frac{e \hbar B}{m}\right] </tex> <tex>\Delta E = E_f - E_i = \left[-\frac{E_0}{3^2} +m_{l_f}\frac{e \hbar B}{2 m} + m_{s_f}\frac{e \hbar B}{m}\right] - \left[-\frac{E_0}{4^2} +m_{l_i}\frac{e \hbar B}{2 m} + m_{s_i}\frac{e \hbar B}{m}\right] </tex>](lib/plugins/latex/images/fb2a98b8452ca392b50be89ecba8ff4679bd0e3f_0.png)
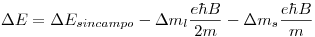
La transición es 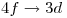 , es decir
, es decir 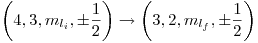
Tenemos que tener en cuenta las reglas de selección, es decir:
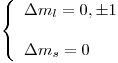
Siendo 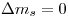 , nos queda:
, nos queda:
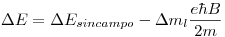
Por lo tanto, en vez de tener una sola longitud de onda, tenemos 3:
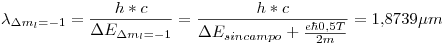
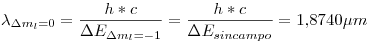

Para saber si esas lineas se podrán apreciar o no, debemos saber la diferencia que hay entre 2 de ellas (consecutivas). Para eso tomamos 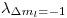 y
y 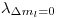 o bien
o bien 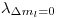 y
y 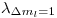 (es lo mismo):
(es lo mismo):
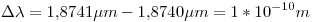
Como el espectómetro tiene una resolución menor (mejor), las líneas serán diferenciables.
Por último, calculamos los momentos magnéticos:
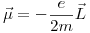
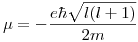
Como  , los valores posibles de l son
, los valores posibles de l son 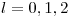 .
.
Por lo tanto, los momentos magnéticos serán:

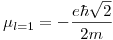
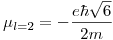
La teoría de Bohr tiene en cuenta un solo número cuántico: 
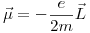
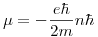
Entonces, según la teoría de Bohr hay un solo momento magnético: