Primer Parcial - 62.15 Física III D
Cátedra: Arcondo
Fecha: Primer Parcial - 1° Cuatrimestre
Día: 20/05/2008
Enunciado
Punto I
Se emite un haz de fotones mediante una transición electrónica entre los niveles  y
y  . Este haz luminoso de potencia
. Este haz luminoso de potencia  incide sobre un metal cuya función trabajo es
incide sobre un metal cuya función trabajo es  , originando la emisión de electrones por efecto fotoeléctrico con rendimiento
, originando la emisión de electrones por efecto fotoeléctrico con rendimiento  (número de electrones emitidos/número de fotones incidentes). Calcular:
(número de electrones emitidos/número de fotones incidentes). Calcular:
- la energía, frecuencia y cantidad de movimiento de los fotones;
- la energía cinética de los fotoelectrones;
- si todos los electrones emitidos llegan al ánodo, calcular la corriente eléctrica que circula por el circuito
Punto II
El electrón de un átomo de hidrógeno se encuentra en un estado excitado. Determinar el número cuántico principal (n) correspondiente a dicho estado, si al pasar al estado fundamental se emiten 2 fotones consecutivos de longitudes de onda 4862 Å y 1215 Å, respectivamente. Indicar a qué transiciones corresponden los fotones emitidos.
Punto III
- Determinar la configuración electrónica (en notación espectroscópica) del
 a
a 
- Suponiendo que no existieran los 2 electrones de menor energía y que el tercero se mantuviera en su subnivel (caso del
 con su electrón remanente en 2s), calcular la energía de ionización del átomo.
con su electrón remanente en 2s), calcular la energía de ionización del átomo. - Experimentalmente la energía de ionización del
 es
es 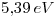 . Si se desprecia la interacción entre electrones, ¿Qué carga efectiva positiva percibe el electrón de valencia?
. Si se desprecia la interacción entre electrones, ¿Qué carga efectiva positiva percibe el electrón de valencia?
Punto IV
Un protón de energía E se encuentra sometido a un potencial como el que muestra la figura. Se sabe que inicialmente la posición del protón está entre 0 y a.
- Escribir la función de onda en todo el espacio y para todo tiempo. (Escribir el sistema de ecuaciones completo pero no resolverlo)
- Representar
 y
y 
- ¿Cuál es la probabilidad de encontrar al protón en la región
 ? (Deje expresada la cuenta)
? (Deje expresada la cuenta) - ¿Qué tiene de peculiar el resultado del punto III?
Resolución
Punto I
Se emite un haz de fotones mediante una transición electrónica entre los niveles  y
y  . Este haz luminoso de potencia
. Este haz luminoso de potencia  incide sobre un metal cuya función trabajo es
incide sobre un metal cuya función trabajo es  , originando la emisión de electrones por efecto fotoeléctrico con rendimiento
, originando la emisión de electrones por efecto fotoeléctrico con rendimiento  (número de electrones emitidos/número de fotones incidentes). Calcular:
(número de electrones emitidos/número de fotones incidentes). Calcular:
- la energía, frecuencia y cantidad de movimiento de los fotones;
- la energía cinética de los fotoelectrones;
- si todos los electrones emitidos llegan al ánodo, calcular la corriente eléctrica que circula por el circuito
La energía de los fotones está dada por la transición. Los fotones que se emiten debido a esa transición tienen energía 
Sabiendo que  , podemos calcular la frecuencia de los fotones emitidos debido a la transición:
, podemos calcular la frecuencia de los fotones emitidos debido a la transición:


De la ecuación de de Broglie  podemos calcular la cantidad de movimiento:
podemos calcular la cantidad de movimiento:


En el efecto fotoeléctrico sabemos que:

Reemplazando obtenemos:


Para el último punto, sabemos que el haz luminoso tiene una potencia de  , es decir, en un segundo se irrandian
, es decir, en un segundo se irrandian  de energía. Como esta energía proviene de los fotones, calculamos cuantos fotones son necesarios por segundo.
de energía. Como esta energía proviene de los fotones, calculamos cuantos fotones son necesarios por segundo.
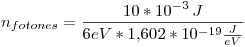

Como el rendimiento es menor a 1, calculamos el número de electrones emitidos (que son los que aportan a la corriente eléctrica):


Siendo que la intensidad de corriente está dada por  y tenemos la cantidad de electrones emitidos por segundo, calculamos la intensidad de corriente:
y tenemos la cantidad de electrones emitidos por segundo, calculamos la intensidad de corriente:


Punto II
El electrón de un átomo de hidrógeno se encuentra en un estado excitado. Determinar el número cuántico principal (n) correspondiente a dicho estado, si al pasar al estado fundamental se emiten 2 fotones consecutivos de longitudes de onda 4862 Å y 1215 Å, respectivamente. Indicar a qué transiciones corresponden los fotones emitidos.
El electrón se encuentra en un estado excitado  , cae al estado excitado
, cae al estado excitado  y luego al estado fundamental (n = 1).
y luego al estado fundamental (n = 1).
Por lo tanto, se observarán 2 fotones consecutivos con longitudes de onda:

y

De la segunda ecuación podemos despejar 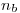 :
:

Si comparamos la primera transición  con la segunda
con la segunda  , vemos que la diferencia
, vemos que la diferencia  es más chica que
es más chica que  , por lo tanto
, por lo tanto  , entonces
, entonces  y
y  . Reemplazando en la ecuación que obtuvimos de
. Reemplazando en la ecuación que obtuvimos de  obtenemos:
obtenemos:

De la misma manera despejamos 

Reemplazando con los valores obtenidos, se desprende que:

Como ya dijimos antes, la primera transición que se ve  es de un fotón con
es de un fotón con  y la segunda
y la segunda  es de un fotón con
es de un fotón con 
Punto III
- Determinar la configuración electrónica (en notación espectroscópica) del
 a
a 
- Suponiendo que no existieran los 2 electrones de menor energía y que el tercero se mantuviera en su subnivel (caso del
 con su electrón remanente en 2s), calcular la energía de ionización del átomo.
con su electrón remanente en 2s), calcular la energía de ionización del átomo. - Experimentalmente la energía de ionización del
 es
es 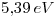 . Si se desprecia la interacción entre electrones, ¿Qué carga efectiva positiva percibe el electrón de valencia?
. Si se desprecia la interacción entre electrones, ¿Qué carga efectiva positiva percibe el electrón de valencia?
Punto IV
Un protón de energía E se encuentra sometido a un potencial como el que muestra la figura. Se sabe que inicialmente la posición del protón está entre 0 y a.
- Escribir la función de onda en todo el espacio y para todo tiempo. (Escribir el sistema de ecuaciones completo pero no resolverlo)
- Representar
 y
y 
- ¿Cuál es la probabilidad de encontrar al protón en la región
 ? (Deje expresada la cuenta)
? (Deje expresada la cuenta) - ¿Qué tiene de peculiar el resultado del punto III?

