NOTA IMPORTANTE: Los siguientes resultados pueden tranquilamente contener errores. Tómalos como una referencia pero no confie totalmente en ellos. Es por ello que se invita a cualquier persona solidaria a modificarlos en caso de ver algo que no corresponda ![]() , y a agregar lo que falte.
, y a agregar lo que falte.
GUÍA 1
Ley de Coulomb
Ejercicio 1
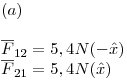
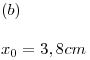
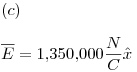
En 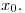 Para la carga negativa es lo mismo. Se trata de un equilibrio inestable ya que si la carga es desplazada de dicha posición la misma no retorna a su origen.
Para la carga negativa es lo mismo. Se trata de un equilibrio inestable ya que si la carga es desplazada de dicha posición la misma no retorna a su origen.
Ejercicio 2
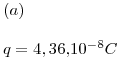
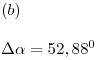
Ejercicio 3
![<tex>(a) \\ \\ \ E_x = \frac{\lambda }{{4\pi \varepsilon _0 }}\left[ {\frac{1}{{\sqrt {\left( {x - \frac{L}{2}} \right)^2 + y^2 + z^2 } }} - \frac{1}{{\sqrt {\left( {x + \frac{L}{2}} \right)^2 + y^2 + z^2 } }}} \right]</tex> <tex>(a) \\ \\ \ E_x = \frac{\lambda }{{4\pi \varepsilon _0 }}\left[ {\frac{1}{{\sqrt {\left( {x - \frac{L}{2}} \right)^2 + y^2 + z^2 } }} - \frac{1}{{\sqrt {\left( {x + \frac{L}{2}} \right)^2 + y^2 + z^2 } }}} \right]</tex>](lib/plugins/latex/images/dd81a4845f275189ce488ac3390a313bad59d14b_0.png)
![<tex>E_y = \frac{\lambda }{{4\pi \varepsilon _0 }}\frac{y}{{y^2 + z^2 }}\left[ {\frac{{x + \frac{L}{2}}}{{\sqrt {\left( {x + \frac{L}{2}} \right)^2 + y^2 + z^2 } }} - \frac{{x - \frac{L}{2}}}{{\sqrt {\left( {x - \frac{L}{2}} \right)^2 + y^2 + z^2 } }}} \right]</tex> <tex>E_y = \frac{\lambda }{{4\pi \varepsilon _0 }}\frac{y}{{y^2 + z^2 }}\left[ {\frac{{x + \frac{L}{2}}}{{\sqrt {\left( {x + \frac{L}{2}} \right)^2 + y^2 + z^2 } }} - \frac{{x - \frac{L}{2}}}{{\sqrt {\left( {x - \frac{L}{2}} \right)^2 + y^2 + z^2 } }}} \right]</tex>](lib/plugins/latex/images/904aa910bc709ac19fa14359d0d86b96ac22d4af_0.png)
![<tex>E_z = \frac{\lambda }{{4\pi \varepsilon _0 }}\frac{z}{{y^2 + z^2 }}\left[ {\frac{{x + \frac{L}{2}}}{{\sqrt {\left( {x + \frac{L}{2}} \right)^2 + y^2 + z^2 } }} - \frac{{x - \frac{L}{2}}}{{\sqrt {\left( {x - \frac{L}{2}} \right)^2 + y^2 + z^2 } }}} \right]</tex> <tex>E_z = \frac{\lambda }{{4\pi \varepsilon _0 }}\frac{z}{{y^2 + z^2 }}\left[ {\frac{{x + \frac{L}{2}}}{{\sqrt {\left( {x + \frac{L}{2}} \right)^2 + y^2 + z^2 } }} - \frac{{x - \frac{L}{2}}}{{\sqrt {\left( {x - \frac{L}{2}} \right)^2 + y^2 + z^2 } }}} \right]</tex>](lib/plugins/latex/images/cc7a27a4d1fc6ee99c0fe3005b65fb54979a73fa_0.png)
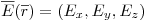
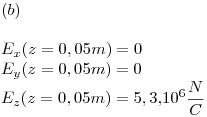
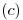
RESOLUCIÓN
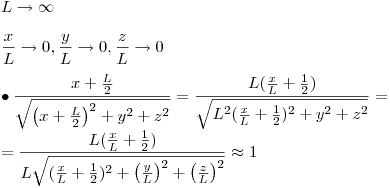
entonces,
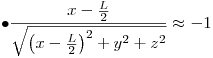
finalmente,
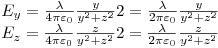
Luego,
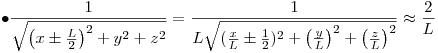
entonces:
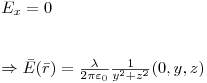
,en coordenadas polares:
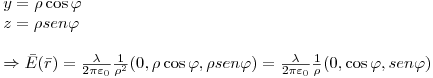
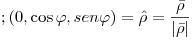
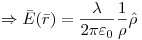
Ejercicio 4
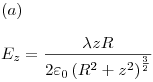
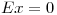
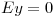
Ejercicio 5
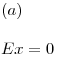
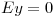
![<tex>E_z = \frac{{\sigma Z}}{{2\varepsilon _0 }}\left[ {\frac{1}{z} - \frac{1}{{\sqrt {R^2 + z^2 } }}} \right]</tex> <tex>E_z = \frac{{\sigma Z}}{{2\varepsilon _0 }}\left[ {\frac{1}{z} - \frac{1}{{\sqrt {R^2 + z^2 } }}} \right]</tex>](lib/plugins/latex/images/dcef87114b23ccbbb5649eae0fa10a08c1249d91_0.png)
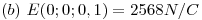
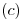
Si z < < R, podemos considerar al caso como a un plano infinito y decir que:
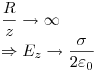
Si z > > R:
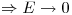
Ejercicio 6
Demostrado en la parte 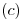 del ej. anterior.
del ej. anterior.
Ejercicio 7
Las cuentas parece que son un quilombo y ni idea como son. Solo sé que en el apunte de EyM de la cátedra se llega a este resultado (sin mostrar las cuentas) usando coordenadas esféricas:
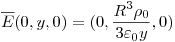
luego por simetría, para r=(x,y,z):
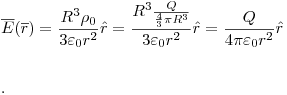
Ley de Gauss
Ejercicio 8
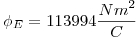
Ejercicio 9
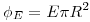
Ejercicio 10
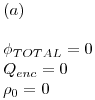
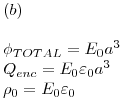
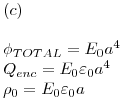
Completar
Ejercicio 11
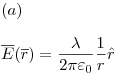
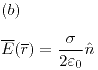
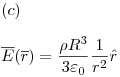
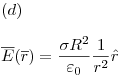
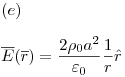
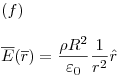
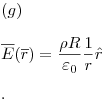
Diferencia de potencial y potencial electrostático
Ejercicio 12
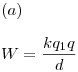
El trabajo no depende del camino que se tome, porque el campo eléctrico es conservativo.
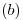
Para el caso más simple tomamos:
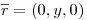 (En realidad no se especifica en donde se encuentra la carga).
(En realidad no se especifica en donde se encuentra la carga).
Como sistema de referencia se eligió al cero entre las dos cargas en la línea que los separa.
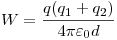
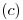
Si 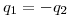
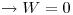 (para el caso más simple)
(para el caso más simple)
Ejercicio 13
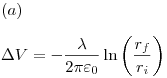
No se pude tomar como referencia al infinito el problema diverge, como en cualquier distribución infinita. ¿Cómo hago para alejarme “infinitamente” de algo “infinito”?. Si reemplazo ri por infinito queda un ln 0 —> diverge.
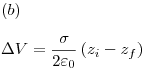
Tampoco se puede tomar como referencia al infinito.
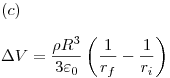
Sí se puede tomar al infinito como referencia.
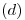
COMPLETAR
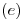
COMPLETAR
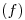
COMPLETAR
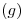
COMPLETAR
Ejercicio 14
Entre los dos planos: 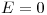
Izquierda del plano izquierdo: 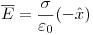
Derecha del plano derecho: 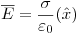
Para el potencial lo mejor es tomar como referencia alguno de los 2 planos e integrar….
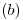
Entre los dos planos: 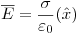
Fuera de los dos planos: 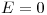
Ejercicio 15
![<tex>(a) \\ \\\Delta V = \frac{{\lambda R}}{{2\varepsilon _0 }}\left[ {\frac{1}{{\sqrt {R^2 + z_f^2 } }} - \frac{1}{{\sqrt {R^2 + } z_i^2 }}} \right]</tex> <tex>(a) \\ \\\Delta V = \frac{{\lambda R}}{{2\varepsilon _0 }}\left[ {\frac{1}{{\sqrt {R^2 + z_f^2 } }} - \frac{1}{{\sqrt {R^2 + } z_i^2 }}} \right]</tex>](lib/plugins/latex/images/0c9535a8b17084c581b7c97f0528a498b58782ef_0.png)
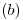
Por definición, el gradiente de una función potencial es igual al campo vectorial:
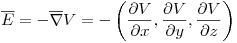
De acuerdo al ejercicio 4 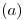 :
:
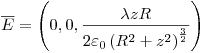
Integrando, se llega al resultado de la parte 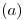 .
.
GUÍA 2
Conductores
(A partir de ahora voy a considerar que a, b, c ,d ,… son radios de menor a mayor en los ejercicios donde aparecen esferas o cilindros con varios radios)
Ejercicio 1
Aplicando la ley de Gauss con una superficie gaussiana de radio r,
-Campo:
r < R:
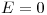
r > R:
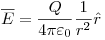
-Potencial:
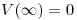
r > R:
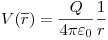
r < R:
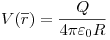
Ejercicio 2
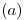
-Campo:
r < a:
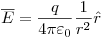
a < r < b:
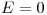
r > b:
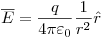
-Potencial:
r > b:
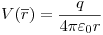
a < r < b:
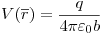
r < a:
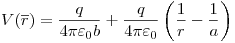
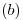
-Campo:
r < a:
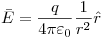
a < r < b:
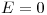
r > b:
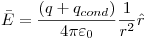
-Potencial:
r > b:
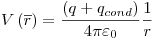
a < r < b:
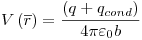
r < a:
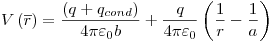
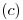
-Campo:
r < a:
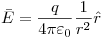
a < r < b:
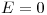
r > b:
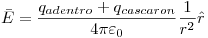
-Potencial:
r > b:
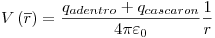
a < r < b:

r < a:
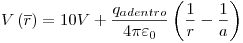
Ejercicio 3
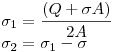
Ejercicio 4
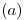
En la cáscara el potencial respecto de tierra (infinito) es:
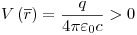
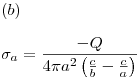
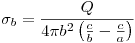
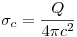
Ejercicio 5
-Campo:
r < a:
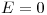
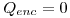
a < r < b:

(Porque el conductor está aislado)
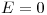
b < r < c:
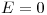
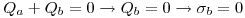
r > c:
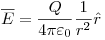
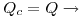
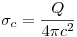
-Potencial:
r > c:
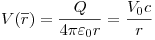
b < r < c:
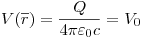
a < r < b:
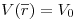
r < a:
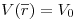
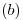
Ahora la diferencia de potencial entre la superficie a y el infinito es 0. Y lo mejor sería tomar como referencia al infinito, entonces el potencial en a sería 0. Ahora también la carga en la superficie a es incógnita.
COMPLETAR
Dieléctricos
Ejercicio 6
La condición que debe cumplirse, cosa que ocurre en la mayoría de los materiales lineales e isótropos, es la siguiente:
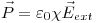
Ejercicio 7
Sabiendo que el campo es uniforme, solo queda trabajar con las diferencias de potencial y las condiciones de frontera.
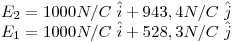
Para D y P se usarían las fórmulas habituales….
Ejercicio 8
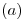
Campo:
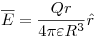 para r < R
para r < R
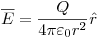 para r > R
para r > R
Potencial:
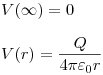 para r > R
para r > R
![<tex>V(r) = \frac{Q}{{4\pi \varepsilon _0 R}} - \frac{Q}{{4\pi \varepsilon R^3 }}\left[ {\frac{{r^2 }}{2} - \frac{{R^2 }}{2}} \right]</tex> <tex>V(r) = \frac{Q}{{4\pi \varepsilon _0 R}} - \frac{Q}{{4\pi \varepsilon R^3 }}\left[ {\frac{{r^2 }}{2} - \frac{{R^2 }}{2}} \right]</tex>](lib/plugins/latex/images/22a8041335045eaf221b91f80509d42b5b6f7d90_0.png) para r < R
para r < R
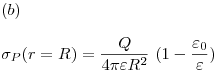
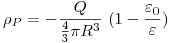
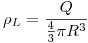

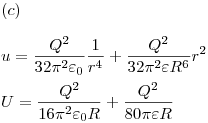
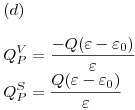
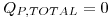
Esto debía dar justamente cero, porque un material dieléctrico sin carga libre es (naturalmente) eléctricamente neutro, y al polarizarse con un campo externo las cargas polarizadas no se desprenden del material, entonces el material sigue siendo neutro, pero con un nuevo campo interno que se opone al externo debido a la forma en que se polarizan sus cargas. Por eso, siempre la carga de polarización total debe dar cero.
hasta aquí llegamos por ahora… estás invitado a seguirlo ![]()