Examen Parcial - 62.03 Física II A B 2º Parcial
Cátedra: Turno 03, Pagnola Día: 15/12/2007
Enunciado
Punto I
En los cuatro casos, los circuitos con una resistencia de 
están inmersos en un campo magnético uniforme entrante que aumenta linealmente con el tiempo razón de 
por segundo. Calcule el flujo del campo en cada caso, la corriente y el sentido de circulación.
; 
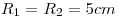
Punto II
Datos:
, 
, 
, 
, 
.
(a) Calcule la impedancia total.
(b) Calcule la corriente que pasa por la fuente.
(c ) Calcule la caída de tensión en el R, L y C.
(d) Calcule la potencia activa y reactiva.
Punto III
Dentro del tubo hay una resistencia conectada a una pila, usada para calentar el agua que hay adentro. La potencia disipada por la resistencia es de 
. La temperatura externa es de 20ºC. Cuál es la temperatura del agua?
Datos: 
, 
, 
, 
, 
, 
Punto IV
En el proceso graficado, conoce 
, 
, 
y 
.
(a) Es un proceso reversible? Justifique.
(b) Calcule las variables termodinámicas en los cuatro puntos.
(c ) Calcule 
, 
y 
para cada caso, explicitando si entrega o recibe calor, realiza o recibe trabajo y si pierde o gana energía interna.
RESOLUCIÓN
Punto III
Por convección, el calor a través del tiempo entregado por el agua está regido bajo la fórmula 
donde 
es la temperatura interna y 
es la temperatura de la cara interna del cilindro. De la misma forma se puede tomar la convección del aire, cuya fórmula queda como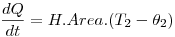 
.
La conducción de calor producida dentro del material que compone el cilindro, está regida por la ecuación:
Al integrar queda que
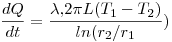
Se despejan las tres ecuaciones:
.
Si sumamos las tres ecuaciones de conducción y convección llegamos a
![<tex>\frac {dQ}{dt} \left [\frac{1}{h_i2 \pi r_1 L} + \frac{1}{h_e 2 \pi r_2 L} + \frac{ln (r_2 / r_1)}{\lambda 2 \pi L} \right ] = \theta _1 - \theta _2</tex>](lib/plugins/latex/images/564595ef0c576446dde75db06b41bd959ba09e3a_0.png "<tex>\frac {dQ}{dt} \left [\frac{1}{h_i2 \pi r_1 L} + \frac{1}{h_e 2 \pi r_2 L} + \frac{ln (r_2 / r_1)}{\lambda 2 \pi L} \right ] = \theta _1 - \theta _2</tex>")
.
Si se reemplazan las variables por los datos provistos por el enunciado, nos queda que 
ºC.
Punto IV
b) del Punto 2 conozco y . Por lo tanto puedo calcular 
con la fórmula de los gases ideales. Entonces
El proceso del punto 2 al 3 es a través de una isoterma, por lo tanto la temperatura en el punto 3 será la misma que en el punto 2. Además contamos con el dato de . Entonces 
De 3 a 4 me muevo por una isobara por la tanto la presión será igual a la calculada en 3. El es dato. Puedo despejar 
. Tenemos 
Por último en el punto 1 la presión es igual que en 3 y el volumen es igual que en 2. La variable termodinámica que nos falta es entonces 