Examen Parcial - 62.03/04. Física II A/B
Cátedra: Perez
Fecha: Segund Parcial - Segundo Oportunidad - Primer Cuatrimestre 2006
Día: xx/07/2006
Enunciado
Punto I
100 espiras cuadradas de  de lado se mueven con una velocidad de
de lado se mueven con una velocidad de  en una región donde hay un campo
en una región donde hay un campo  uniforme, normal y entrante de
uniforme, normal y entrante de  .
Determine y grafique la fem inducida en función de la posición, cuando está entrando y cuando ya ingresó.
.
Determine y grafique la fem inducida en función de la posición, cuando está entrando y cuando ya ingresó.
Punto II
Se tiene un circuito RLC serie cuyas: 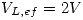 ,
,  ,
,  y
y 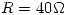
- Dibuje el diagrama fasorial
- Calcule la
 de la fuente
de la fuente - Calcule la
 y la diferencia de fase entre la fuente y la corriente.
y la diferencia de fase entre la fuente y la corriente. - Calcule el triángulo de potencias.
Punto III
Parte a
Calcule las autoinductancias de cada bobina y la mutua del siguiente circuito.
Datos:

Parte b
Para la siguiente configuración calcule  y coloque los bornes homólogos.
y coloque los bornes homólogos.
Punto IV
Una cañería cilíndrica transporta un fluido a alta temperatura, siendo la ambiente 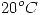 . En régimen estacionario la cantidad de calor por unidad de tiempo y longitud es de
. En régimen estacionario la cantidad de calor por unidad de tiempo y longitud es de  .
.
- Calcular la temperatura del fluído que transporta.
- Calcular la temperatura extrema de las paredes.
- Calcular el gradiente de temperaturas para

Datos:  ,
,  ,
, 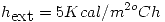 ,
,  y
y  .
.
Punto V
En el laboratorio en la práctica de corrientes dependientes del tiempo.
- ¿Cómo se encontró la frecuencia de resonancia?, ¿Cómo midió el Q?, ¿Qué tipo de circuito era?.
- Para armar un transformador, ¿qué entrehierro utilizaría (de los usados en la práctica) para obtener la mejor relación entrada-salida?.
Resolución
Punto I
En la figura se muestran un esquema del problema, en el cual:  ,
,  y
y 
Cuando la espira está entrando en la región de campo magnético (figura b), entonces el flujo es sólo desde  en adelante, por lo tanto el flujo para 1 espira es:
en adelante, por lo tanto el flujo para 1 espira es:

El flujo total (para todas las espiras) es: 
Ahora calculamos 
La ley de Faraday-Lenz dice que:  , por lo tanto
, por lo tanto 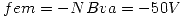
Como nos dio negativo eligiendo la normal  entonces la corriente inducida circulará como
entonces la corriente inducida circulará como  , es decir, en sentido antihorario en el dibujo.
, es decir, en sentido antihorario en el dibujo.
Cuando la espirá ya entró en la región el flujo sobre una espira es:

y por lo tanto al no depender del tiempo, no inducirá ninguna corriente.
Entonces: 
Punto II
El diagrama fasorial que resulta de los datos es el siguiente (cada división de los ejes representa 1V):
Para calcular la tensión de la fuente usamos las propiedades de Pitágoras:

Para calcular la corriente efectiva que circula podemos usar la propiedad de las resistencias:  Entonces:
Entonces: 
La diferencia de fase es el ángulo  de la figura:
de la figura: 
Para el triángulo de potencias usamos:


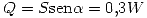
Punto III
Primero debemos calcular el campo que generaría una corriente I en cada bobina y luego ver el flujo que genera en la otra.
Si aplicamos Ampère a la primer bobina:

Lo mismo para la otra bobina: 
El flujo de 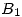 sobre si mismo es
sobre si mismo es  y para la otra es:
y para la otra es:  .
.
Y el flujo que hace el campo 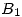 sobre la segunda bobina es:
sobre la segunda bobina es:  .
.
Sabiendo que: 
Entonces:
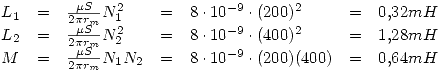
Parte b
ATENCIÓN: Hay un error en el dibujo. El borne de la derecha debería haber sido dibujado en la parte inferior.  Alguien con tiempo/ganas por favor edítelo.
Alguien con tiempo/ganas por favor edítelo.
editado. — sebastian_grodsinsky
Son sustractivos pues si suponemos una corriente en el sentido de la figura, produciría un campo horario en la primer bobina y uno antihorario en la segunda.

Punto IV
Considerando primero la convección de  a
a  tenemos:
tenemos:

Ahora considerando la conducción en la pared:

Por último la convección de la pared 2 al  :
:

Sumando los tres resultados obtenemos:  , donde
, donde  , la resistencia térmica de la pared, es:
, la resistencia térmica de la pared, es:
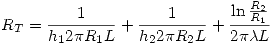
En este caso al reemplazar los datos obtenemos:  , por lo tanto
, por lo tanto 
Las temperaturas extremas de las paredes se calculan:



Idem para  que obtenemos
que obtenemos 
Para obtener el gradiente térmico se hace:
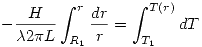

En  se obtiene:
se obtiene:

Discusión
Error en el dibujo de bornes homólogos
me parece que los bornes homologos estan mal establecidos, porque la corriente es entrante por ambos pero son sustractivos. — sebastian_grodsinsky
Gracias por avisar. Ya puse una aclaración. Restaría que alguien rehaga el dibujo.
— Fhran 2007/06/29 12:52
Ya está. Dejo el mensaje de fhran que explica como subir y cambiar imagenes:
Buenísimo. Te explico como hacer.
En el modo edición, hacele click al botón que tiene un cuadro y está a la izquierda del botón con un smiley Smile.
Se te abre una ventana que te muestra todos los archivos subidos para esa sección.
Si le hacés click a alguno, se cierra y te inserta el código en tu artículo.
Al final de todo te deja subir archivos nuevos.
Una vez subido, sólo tenés que reemplazar en el artículo, el código del dibujo anterior, por el nuevo que subiste.
Saludos.
Fhran.
— sebastian_grodsinsky
Posible error en el Punto 1
Me parece que el problema 1 esta mal resuelto. Cuando se deriva el flujo en el momento que la espira esta entrando al campo, se esta conciderando que la velocidad de la misma es constante lo cual no es cierto. Para poder determinar como varia la velocida de la espira necesitamos conocer su resistencia, la cual no es dato del problema. El problema estaria bien resuelto solo en el caso en que la resistencia de las espiras fuera infinita y por lo tanto no hay circulacion de corriente. — rulo86 2007/07/09 13:23
Cuando en este tipo de problemas, el enunciado te dice que la velocidad es de 5 m/s, tenés que interpretar que se mantiene constante sin importar las fuerzas resultantes que aparecen. Si no esperaran eso, el problema, así planteado, es muy inocente. Pero tenés razón en que si una espira viene con velocidad constante y entra en la zona de donde existe, la variación de flujo produce una corriente, y los tramos de conductor con corriente que vayan entrando al campo, irán experimentando una fuerza que se opone al movimiento.
— Fhran 2007/07/09 14:26





