Parcialito - 62.01. Física 1
Cátedra: Lombardi
Fecha: 1º Cuatrimestre 2009
Enunciado
Punto I
¿Qué parámetros se varían en la práctica de péndulo?
Punto II
¿Desde dónde se mide la longitud del hilo?
Punto III
¿Qué se calcula en el método estático?
Punto IV
Dada la expresión 
Resolución
Punto I
La amplitud, la masa y la longitud del hilo
Punto II
El hilo se mide desde donde se cuelga hasta el centro del cuerpo colgado en el otro extremo.
Punto III
Se calcula la constante elástica. Primero se le pone una masa 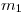 y la ecuación toma la siguiente forma:
y la ecuación toma la siguiente forma:
 , donde
, donde 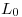 : longitud natural y
: longitud natural y  : longitud que tomó el resote a causa de
: longitud que tomó el resote a causa de 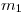
Luego se le suma una masa 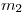 , por lo que el resorte adquiere una nueva longitud
, por lo que el resorte adquiere una nueva longitud  :
:
 Restando las dos ecuaciones anteriores, obtenemos:
Restando las dos ecuaciones anteriores, obtenemos:

De ésta forma la ecuación nos queda independiente de 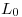 que es una longitud “poco precisa”.
que es una longitud “poco precisa”.
De manera más general, la ecuación es:

Punto IV