2006 - Cátedra Sacerdoti

Enunciado

Dado $<tex>F(z) = \frac{1}{{2\pi }}\int_0^{2\pi } {e^{2z\sin t} dt} </tex>$
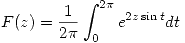
1. Analizar para que valores de z es Holomorfa.
2. Desarrollarla en Serie de Laurent en el V(0).
.
1. Hallar la distribución de potencial P en el interior del circulo representado en la figura.
2. Hallar las lineas equipotenciales.
3. Hallar las lineas de campo.
Calcular por residuos: $<tex>\int_{2 - i\infty }^{2 + i\infty } {\frac{{e^{z.t} }}{{(z - 1)^2 }}dz}</tex>$

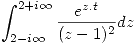
Dada $<tex>F(z) = \frac{1}{{z(z - 1)}}e^{\frac{1}{{z - 1}}}</tex>$ :
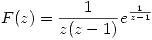1. Analizar los puntos singulares de 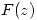$<tex> F(z)</tex>$ en el conjunto complejo extendido.
2. Desarrolarla en serie de Laurent en el V(1).