Tabla de Contenidos
Integrador 8/03/2006 - Cátedra Isaacson
Enunciado
- Resolver utilizando Transformada de Laplace:
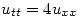 ,
,  ,
, 
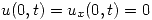 ,
, 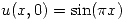 ,
, 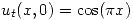
Hallar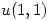 .
. - Se sabe que
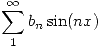 es la Serie de Fourier de
es la Serie de Fourier de 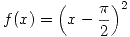 ,
, ![<tex>x \in \left[ 0 , p \right]</tex> <tex>x \in \left[ 0 , p \right]</tex>](lib/plugins/latex/images/da0999eea2bb236c3ed2426a77da8a407edbb2e9_0.png) .
.- Determinar
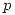 .
. - Graficar la función a la que converge la Serie en
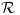 y determinar el tipo de convergencia.
y determinar el tipo de convergencia. - ¿En cuántos puntos del intervalo
![<tex>\left[ 0 , 3 \pi \right]</tex> <tex>\left[ 0 , 3 \pi \right]</tex>](lib/plugins/latex/images/615f513c78a785a4bf8e1d6f58f972e9fc398616_0.png) se anula la serie?
se anula la serie?
- Si las transformadas de
 ,
, 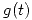 y
y 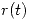 son
son 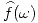 ,
, 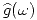 y
y 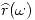 respectivamente, mostrar que la solución de la ecuación
respectivamente, mostrar que la solución de la ecuación
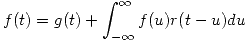
está dada por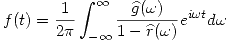 .
.
Establecer las hipótesis necesarias. - Demostrar que
![<tex>\mathcal{Z} \left[ x(n) \ast y(n) \right] = X(z) Y(z)</tex> <tex>\mathcal{Z} \left[ x(n) \ast y(n) \right] = X(z) Y(z)</tex>](lib/plugins/latex/images/6a385db77ee15d3ec587b6643cde120f1fd41a26_0.png) .
. - Demostrar que si
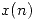 e
e 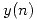 son dos señales causales (esto es
son dos señales causales (esto es 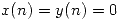 si
si 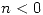 ), entonces:
), entonces:
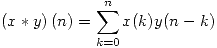 .
. - Usar el punto II para demostrar que si
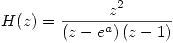 ,
, 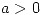 ,
,  , entonces
, entonces 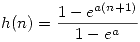 .
.
Resolución
- 1
- 2
- 3
- 4
- I
![<tex>\mathcal{Z} \left[ x(n) \ast y(n) \right] = \sum_{n = - \infty}^{\infty} \left[ x(n) \ast y(n) \right] z^{-n} = \sum_{n = - \infty}^{\infty} \left[ \sum_{k = - \infty}^{\infty} x(k)y(n-k) \right] z^{-n}</tex> <tex>\mathcal{Z} \left[ x(n) \ast y(n) \right] = \sum_{n = - \infty}^{\infty} \left[ x(n) \ast y(n) \right] z^{-n} = \sum_{n = - \infty}^{\infty} \left[ \sum_{k = - \infty}^{\infty} x(k)y(n-k) \right] z^{-n}</tex>](lib/plugins/latex/images/1ccf194b9d306df552ac7fdbd7567cdf6929b799_0.png)
- Intercambiando el orden de las sumatorias (no se como probar que esto es válido, es un truco algebraico):
![<tex>\sum_{k = - \infty}^{\infty} \left[ \sum_{n = - \infty}^{\infty} x(k)y(n-k) z^{-n} \right] = \sum_{k = - \infty}^{\infty} x(k) \left[ \sum_{n = - \infty}^{\infty} y(n-k) z^{-n} \right]</tex> <tex>\sum_{k = - \infty}^{\infty} \left[ \sum_{n = - \infty}^{\infty} x(k)y(n-k) z^{-n} \right] = \sum_{k = - \infty}^{\infty} x(k) \left[ \sum_{n = - \infty}^{\infty} y(n-k) z^{-n} \right]</tex>](lib/plugins/latex/images/da2bb2887b2f874dbd4328095986181dd70abc33_0.png)
- Haciendo el cambio de variable
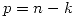 :
:
![<tex>\sum_{k = - \infty}^{\infty} x(k) \left[ \sum_{p = - \infty}^{\infty} y(p) z^{-(p+k)} \right] = \sum_{k = - \infty}^{\infty} x(k) z^{-k} \left[ \sum_{p = - \infty}^{\infty} y(p) z^{-p} \right] = X(z)Y(z)</tex> <tex>\sum_{k = - \infty}^{\infty} x(k) \left[ \sum_{p = - \infty}^{\infty} y(p) z^{-(p+k)} \right] = \sum_{k = - \infty}^{\infty} x(k) z^{-k} \left[ \sum_{p = - \infty}^{\infty} y(p) z^{-p} \right] = X(z)Y(z)</tex>](lib/plugins/latex/images/941d16bc27e10f1aef1747076fdb78bf454ac040_0.png)
- II
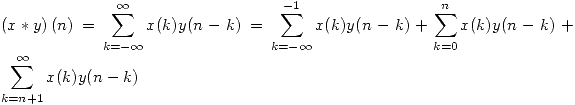
- En el último miembro, el primer término se anula porque
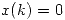 para
para  y el tercer término se anula porque
y el tercer término se anula porque 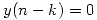 para
para 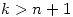 . Entonces nos queda:
. Entonces nos queda: