Tabla de Contenidos

Examen Parcial - 61.07. Matemática Discreta - 24/11/2012

Cátedra: Todas
Fecha: Segunda Oportunidad - 2º Cuatrimestre 2012
Día: 24/11/2012

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Punto I

Sean los enunciados abiertos: p(n): “n es impar”, q(n): ”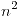<tex>n^2</tex> es impar” con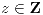 <tex>z \in \mathbf{Z}</tex>

Escribir en lenguaje simbólico las siguientes proposiciones, analizar su valor de verdad e indicar cuáles son equivalentes:

  1. Un entero es impar sólo si su cuadrado es impar.
  2. Que un entero sea impar es condición necesaria para que su cuadrado también lo sea.
  3. El cuadrado de cualquier entero impar es impar.
  4. Existen algunos enteros cuyos cuadrados son impares.
  5. Todo entero con cuadrado par es par.
  6. Un entero es impar sólo si su cuadrado también es impar.

Punto II

Se disponen de n fósforos para formar palabras con las letras I (un fósforo) y con la letra V (dos fósforos). Sea 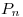<tex>P_n</tex> el número de palabras distintas que se pueden formar con n fósforos.

  1. Hallar una relación de recurrencia para los <tex>P_n</tex>.
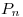  2. Resolver la ecuación del homogéneo del punto anterior igualada a <tex> f(n) = 3\cdot 2^n</tex>

Punto III

Un examen consta de 15 ejercicios. Cada ejercicio se clasifica con Bien, Mal o 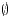<tex>\emptyset</tex>

Se define la relación: 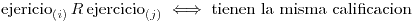<tex>\text{ejericio}_{(i)}\, R\, \text{ejercicio}_{(j)} \iff \text{tienen la misma calificacion}</tex>

  1. Probar que es una relación de equivalencia.
  2. Determinar el conjunto cociente. ¿Cuántas clases de equivalencia hay? ¿Cuántas serían si un alumno responde todas las preguntas?

Punto IV

En 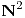<tex>{\mathbf{N}}^2</tex> se defina la siguiente relación <tex>(x,y) R (u,v) \iff x|u \wedge v=y 2^k</tex> con <tex> k \in \mathbf{N}_0</tex>

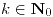
  1. Probar que es una relación de orden.
  2. ¿Es un orden total? Justificar.
  3. Hallar los elementos particulares del conjunto <tex>B=\{ (x,y) \in \mathbf{N}^2: 1\ge x\ge 3 \wedge 1\ge y\ge 2 \}</tex>

Punto V

  1. En un Álgebra de Boole si 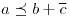<tex>a\preceq b + \overline{c}</tex> entonces ¿es posible que <tex>a \not\preceq b</tex>?
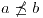  2. En un Álgebra de Boole, demostrar que <tex>a\cdot[b+\overline{a\cdot b} = a \iff b + \overline{a} = 1</tex>
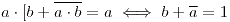
  3. Simplificar la función booleana: <tex> f(x,y,z) = \overline{x} + y + [(y+z)\overline{(x+z)}]</tex> y construir un circuito usando solamente compuertas NAND binarias (dos entradas).

Resolución

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.