Examen (Parcial) - 61.07. Matemática Discreta
Cátedra: todas
Fecha: 1er Oportunidad - (1er Cuatrimestre) 2008
Día: 31/05/2008
Enunciado
1 Sea  un conjunto y
un conjunto y  una relación de orden en
una relación de orden en  que tiene la siguiente propiedad: “Para todo par de elementos
que tiene la siguiente propiedad: “Para todo par de elementos 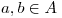 siempre existen:
siempre existen: 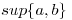 y
y 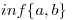 ”
”
Probar que son equivalentes:
a) 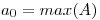
b) Para todo 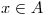 se tiene
se tiene 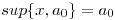
c) Para todo 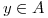 se tiene
se tiene 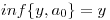
2 Se define en 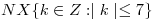 la siguiente relación
la siguiente relación  :
: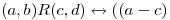 es múltiplo de
es múltiplo de 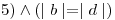
a) Probar que  es una relación de equivalencia.
es una relación de equivalencia.
b) Hallar: 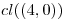 y
y 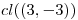
c) ¿Cuantos elementos tiene el conjunto cociente?
3 Sea  un algebra de Boole.
un algebra de Boole.
a) Pruebe que: 
b) Enunciar y probar la propiedad dual de la del item a.
c) Demostrar que para todo 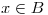 se tiene
se tiene 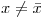 .
.
4 Dada la función booleana: 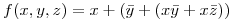
a) Encontrar su forma normal disyuntiva.
b) Simplificarla algebraicamente.
c) Hallar un circuito que la represente utilizando solo compuertas NAND.
5 a) Enunciar el principio de inducción.
b) Probar, usando el principio de induccion, que en toda fila de dos o más personas, si la primera es una mujer y la última un varón, en algún lugar de la fila hay una mujer y un varón consecutivos.
Resolución
Punto III
a) Pruebe que: 
Primero pruebo que 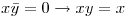
Entonces 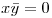 es mi hipótesis , y
es mi hipótesis , y  es mi tesis.
es mi tesis.
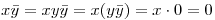 y queda demostrado que
y queda demostrado que 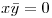
Ahora debo probar que 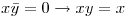
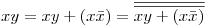
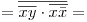
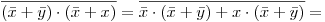
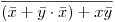 por hip.
por hip. 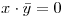 y por ley de absorción
y por ley de absorción 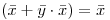 entonces:
entonces:
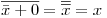
Entonces queda demostrado 
b) La propiedad dual se obtiene reemplazado los +/. por ./+ y los 0 por 1, con lo que nos quedaría:

Al ogual que antes debemos probar ambos sentidos de la condición.
Considero como hipótesis 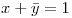 y trato de probar mi tesis
y trato de probar mi tesis 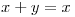
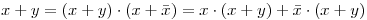 , por ley de absorción
, por ley de absorción 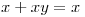 entonces:
entonces:
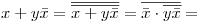
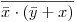 , por hip.
, por hip. 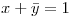 , entonces:
, entonces:
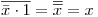 , queda demostrado
, queda demostrado 
Ahora pruebo 
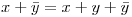 , por ley de inversos
, por ley de inversos 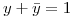 , entonces:
, entonces:
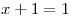 y demostre que
y demostre que  .
.
Queda así demostrado: 