Examen Parcial - 61.07. Matemática Discreta

Cátedra: Todas
Fecha: Primera Oportunidad - Primer Cuatrimestre 2003
Día: 14/06/2003

1. Encontrar todas las soluciones, si existen, del siguiente sistema de ecuaciones en un álgebra de Boole:
2. Dada la ecuacion de recurrencia:
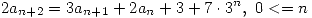
   1. Encontrar todas las soluciones
   2. ¿Existe una solución tal que a0 = 10 y a1 = -1?
3. Sea 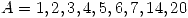. Para cada 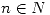se define . Sea la siguiente relación:
   1. Probar que es una relacion de orden en A
   2. ¿Cuáles son los elementos maximales y minimales de A?
   3. Si B = {4,5,6,7}, encontrar todos los elementos particulares de B
   4. Si C = {4,5,6}, encontrar todos los elementos particulaeres de B
4. Dadas las siguientes premisas:
   • Sólo si gano mucho dinero, estudio leyes
   • Viajaré mucho si estudio arqueología
   • Si gano mucho dinero o viajo mucho, no me decepciono
   • Estoy decepcionado
   1. Indicar con cuál de las siguientes conclusiones se obntiene un razonamiento válido y con cuál inválido, justificando su respuesta. Para los razonamientos válidos presentar una demostración formal.
   • G1: No estudio leyes ni arqueología
   • G2: Estudio leyes y arqueología
5. Definir una función booleana que de por resultado “1” únicamente en los casos que se verifiquen las siguientes igualdades simultanáneamente:
   • Presentar su expresión simplifacada y la forma SP