Tabla de Contenidos
Examen Parcial - 61.07. Matemática Discreta - 29/10/2011
Cátedra: Todas
Fecha: 1ra Oportunidad - (2do Cuatrimestre) 2011
Día: 29/10/2011
Esta página está incompleta; podés ayudar completando el material.
Enunciado
Punto I
- Sea
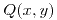 la sentencia, definida en Z ”
la sentencia, definida en Z ”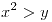 ” . ¿Cuál es el valor de verdad de:
” . ¿Cuál es el valor de verdad de: 


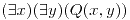 ?
?
- Utilizando cuantificadores y predicados con una variable, exprese:
- Hay un estudiante de esta clase que no tiene teléfono celular.
- Todo estudiante de Ingeniería Informática necesita un curso de Matemática Discreta.
Punto II
Si 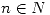 , se llama cadena ternaria de longitud
, se llama cadena ternaria de longitud 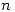 , a una n-upla que sólo contiene los números 0,1 y 2.
, a una n-upla que sólo contiene los números 0,1 y 2.
- Determinar la relación de recurrencia para una sucesión (
 ). donde
). donde  es la cantidad de cadenas ternarias de longitud
es la cantidad de cadenas ternarias de longitud 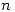 que no poseen dos ceros consecutivos. Determine, también, los valores iniciales.
que no poseen dos ceros consecutivos. Determine, también, los valores iniciales. - Resolver la dada en 1).
- Calcular, utilizando lo obtenido en 2),
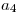 .
.
Punto III
Demostrar, utilizando el principio de inducción, que en un conjunto de 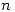 elementos hay
elementos hay  subconjuntos de exactamente dos elementos, si
subconjuntos de exactamente dos elementos, si  . Exprese claramente cual es la proposición que debe probar.
. Exprese claramente cual es la proposición que debe probar.
Punto IV
- Probar, sin utilizar la noción de átomo, que no existe un álgebra de Boole que tenga exactamente tres elementos.
- Hallar la forma normal disyuntiva de la función booleana dada por:


y representarla en un circuito que tenga solamente compuertas NAND (con sólo dos entradas).
Punto V
Si  , se define en
, se define en  las siguientes relaciones:
las siguientes relaciones:
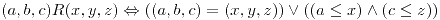

- Determinar si son relaciones de orden o de equivalencia.
- Para todas las que sean relación de equivalencia, hallar todas las clases y cuántos elementos tiene cada una.
- Para todas las que sean relación de orden, hallar todos los elementos particulares de
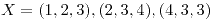
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.