Tabla de Contenidos
Examen Final - 61.07. Matemática Discreta - 29 de Febrero de 2012
Fecha: Oportunidad 5 - Verano 2012
Día: 29/02/2012
Enunciado
Punto I
-
- Definir árbol generador minimal. Dar una condición necesaria y suficiente para su existencia, y justificar.
- Explicar paso a paso un algoritmo para la obtención de un árbol generador minimal, y justificar que se obtiene lo buscado.
Punto II
- Definir árbol generador.
- Demostrar que si todos los árboles generadores de
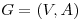 contienen la arista
contienen la arista 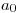 , el grafo
, el grafo 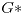 que se obtiene al quitar la arista
que se obtiene al quitar la arista 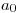 de
de 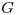 , no es conexo.
, no es conexo. - Demostrar que si un grafo
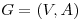 tiene un único árbol generador,
tiene un único árbol generador, 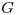 es árbol.
es árbol.
Punto III
- Para un conjunto

- Definir relación de orden.
- Definir todos los elementos particulares de una relación de orden.
- Demostrar que si
 tiene un
tiene un 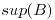 , éste es único.
, éste es único. - Dar un ejemplo de un orden con 3 elementos maximales y 2 elementos minimales, todos diferentes.
Punto IV
- Definir red de transporte, flujo, valor de flujo, corte, y capacidad de corte.
- Definir flujo maximal y corte minimal
- Probar que para cualquier corte
 en una red de transporte con un flujo
en una red de transporte con un flujo 
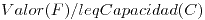 .
. - ¿Qué significa que se de la igualdad del item anterior?
Punto V
- Sean dos álgebras de Boole
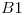 y
y 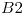 , y
, y 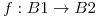 un isomorfismo entre las dos algebras (definir concepto de isomorfismo)
un isomorfismo entre las dos algebras (definir concepto de isomorfismo)- Demostrar que
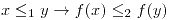
- Sea
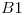 un algebra de Boole formada por los divisores enteros positivos de 105 y
un algebra de Boole formada por los divisores enteros positivos de 105 y ![<tex>B2=(P[A],\cap,\cup,\bar{ },\emptyset,A)</tex> <tex>B2=(P[A],\cap,\cup,\bar{ },\emptyset,A)</tex>](lib/plugins/latex/images/3904235cd2ff407b44d254ee2233192dbdb786d7_0.png) con
con 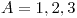 . Se define:\\
. Se define:\\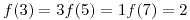
- Definir
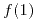 y
y 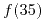
- Dar los atomos de
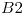
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.