materias:61:07:final_03_20130710_x
Tabla de Contenidos

Examen Final - 61.07. Matemática Discreta - 10/07/2013

Cátedra: Todas
Fecha: Segunda Oportunidad - Invierno 2013
Día: 10/07/2013

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Punto I

Dar el valor de verdad de las siguientes proposiciones. Justificar su respuesta.

  1. Existe un grafo dirigido de 3 vértices, no euleriano tal que cada vértice tiene grado interior igual al grado exterior.
  2. El grafo de la figura admite al menos 2 árboles generadores mínimos con todas sus aristas distintas.
  3. Todo grafo conexo de 5 vértices y 6 aristas es un árbol.

Punto II

Probar que:

  1. Si un grafo es conexo y tiene al menos dos vértices, tales que el grado de uno de ellos es igual a 1, y el de los demás es mayor (estricto) a 2, entonces el grafo tiene al menos un ciclo.
  2. Si un Grafo conexo y acíclico, entonces <tex>|A| = |V|^{-1}</tex>.

Punto III

Dado un grafo G cuya matriz de adyacencia es:

<tex>A= \begin{matrix} & V_1 & V_2 & V_3 & V_4 & V_5 & V_6 \\ V_1 & 0 & 1 & 1 & 0 & 1 & 1 \\ V_2 & 1 & 0 & 1 & 1 & 0 & 1 \\ V_3 & 1 & 1 & 0 & 1 & 1 & 0 \\ V_4 & 0 & 1 & 1 & 0 & 1 & 0 \\ V_5 & 1 & 0 & 1 & 1 & 0 & 1 \\ V_6 & 1 & 1 & 0 & 0 & 1 & 0 \\\end{matrix}</tex>

  1. Analizar si es un grafo de Euler. Justificar la respuesta. Y en caso afirmativo hallar el camino o circuito.
  2. Analizar si es un grafo de Hamilton.
  3. Si se quita el vértice V2 y las aristas incidentes en él ¿El grafo resultante es isomorfo al del dibujo? ¿Y si se quita V3? Justifique.

Acá había dibujado un grafo con 5 vértices: a,b,c,d,e con adyacencias:

Punto IV

  1. Determinar el resultado de multiplicar la matriz A consigo misma n veces, siendo <tex>A = \left (\begin{matrix} 1 & -1\\ -1 & 1\end{matrix}\right )</tex>. Probar por inducción tal resultado.
  2. Dar el valor de verdad de: “Si R y S son dos relaciones de orden, entonces <tex> R \cap S</tex> y <tex> R \cup S</tex> también son relaciones de orden”.

Punto V

Se define en 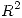<tex>R^2</tex> la siguiente relación: <tex>(x,y)R(w,z) \iff (x-y)^2 = (w-z)^2</tex>

  1. Demostrar que se trata de una relación de equivalencia.
  2. Calcular <tex>cl(1,2)</tex>, <tex>cl(-1,2)</tex>, <tex>cl(2,2)</tex> y <tex>cl(0, \sqrt{2})</tex>, y graficarlas en el plano.
  3. Escribir el conjunto cociente. ¿Cómo sería el conjunto cociente si en vez de estar trabajando en los pares ordenados de números reales, estuviéramos trabajando con los pares ordenados de números naturales?

Resolución

Punto I

  1. VERDADERO: Un grafo con tres vértices aislados cumple.
  3. FALSO: Como contraejemplo, considerar un circuito de 5 vértices, y que dos de ellos estén conectados con una arista más

Punto II

(1)

Si existe en el grafo algún lazo, existe entonces un ciclo.
Si existen aristas paralelas, entonces existe también un ciclo.
Supongamos entonces un grafo sin lazos y sin aristas paralelas, de dos vértices <tex>v_1</tex> y <tex>v_2</tex> unidos por una arista. Si se quiere que <tex>gr(v_2)>2</tex> entonces se agregan dos vértices más, cada uno unido a <tex>v_2</tex> por separado. Para cada uno de estos nuevos vértices de grado 1, se agregan dos vértices más, también unidos por separado. Siguiendo esta lógica se obtiene un árbol cuyas hojas, claramente, tienen un grado igual a 1. Pero por ser conexo, si se agrega una arista entre dos vértices existentes, se está agregando un segundo posible camino entre estos dos vértices, lo que lleva seguramente a un ciclo.

(2)

Dada la hipótesis, por cada vértice que se agrega al grafo, se agrega una y sólo una arista, ya que si se agregasen dos, por la hipótesis de conexividad, se formaría un segundo camino entre los dos vértices adyacentes, es decir un ciclo. La diferencia entre <tex>|A|</tex> y <tex>|V|</tex> se debe a que, cuando se agrega un vértice a un grafo vacío no se agrega una arista.

Punto III

(1)

Es un grafo de Euler porque existen sólo dos vértices de grado impar (aquellos que tienen una cantidad impar de 1's en su fila o columna).
Un camino podría ser <tex>v_4 \rightarrow v_5 \rightarrow v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_1 \rightarrow v_6 \rightarrow v_2 \rightarrow v_4 \rightarrow v_3 \rightarrow v_5 \rightarrow v_6</tex>.

(2)

Es un grafo de Hamilton porque existe un camino y/o un ciclo hamiltoniano. Por ejemplo: <tex>v_4 \rightarrow v_5 \rightarrow v_6 \rightarrow v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4</tex>.

(3)

Sí es isomorfo porque, siendo <tex>V_{G'}</tex> el grafo sin el vértice 2 y <tex>V_D</tex> el dibujado, <tex>\exists f:V_{G'} \longrightarrow V_{D}</tex> biyectiva.
Por ejemplo:
<tex>f(v_1)=c\\ f(v_3)=e\\ f(v_4)=d\\ f(v_5)=a\\ f(v_6)=b</tex>
Y para cada <tex>\{v, w\} \in A_{G'}</tex> corresponde que <tex>\{f(v), f(w)\} \in A_{D}</tex>.
Lo mismo sucede reemplazando el vértice 3 por el vértice 2 (analizarlo).

Punto IV

(1)

Elevando <tex>A</tex> al cuadrado y al cubo, se puede especular que, genéricamente,

<tex>A^n = \left( \begin{array}{cccc} 2^{n-1} & -2^{n-1} \\ -2^{n-1} & 2^{n-1}\end{array} \right)</tex>

Probaremos entonces que

<tex>A^n = \left( \begin{array}{cccc} 2^{n-1} & -2^{n-1} \\ -2^{n-1} & 2^{n-1}\end{array} \right)\longrightarrowA^{n+1} = \left( \begin{array}{cccc} 2^{n} & -2^{n} \\ -2^{n} & 2^{n}\end{array} \right)</tex>

Comenzamos analizando que
<tex>A^{n+1} = A^n \times A </tex>

Y, usando la hipótesis y el valor conocido de <tex>A</tex>:

<tex> A^{n+1} = \left( \begin{array}{cccc} 2^{n}/2 & -2^{n}/2 \\ -2^{n}/2 & 2^{n}/2\end{array} \right) \cdot\left( \begin{array}{cccc} 1 & -1 \\ -1 & 1\end{array} \right)=\\= \frac{1}{2}\left( \begin{array}{cccc} 2^{n} & -2^{n} \\ -2^{n} & 2^{n}\end{array} \right) \cdot\left( \begin{array}{cccc} 1 & -1 \\ -1 & 1\end{array} \right) =\frac{1}{2}\left( \begin{array}{cccc} 2^n + 2^n & -2^n - 2^n \\ -2^n - 2^n & 2^n + 2^n\end{array} \right) =\\= \frac{1}{2}\left( \begin{array}{cccc} 2\times2^n & -2\times2^n \\ -2\times2^n & 2\times2^n\end{array} \right) =\left( \begin{array}{cccc} 2^n & -2^n \\ -2^n & 2^n\end{array} \right)</tex>

Ahora falta el primer caso, con <tex>n=1</tex>:

<tex> A^1 =\left( \begin{array}{cccc} 2^0 & -2^0 \\ -2^0 & 2^0\end{array} \right) =\left( \begin{array}{cccc} 1 & -1 \\ -1 & 1\end{array} \right)</tex>

Y confirmamos que la igualdad especulada al principio se confirma <tex>\forall n \geq 1</tex>.

(2)

La proposición dada resulta ser falsa. La idea es ir analizando por separado la reflexión, antisimetría y transitividad de las relaciones <tex>R \cap S</tex> y <tex>R \cup S</tex>. Cuando se analiza la antisimetría de <tex>R \cup S</tex> no se puede garantizar que <tex>x=y</tex> por lo que no es garantía de que <tex>R \cup S</tex> sea antisimetrica, es decir que no es de orden. Y como la tesis de la condición esta compuesta por una conjunción ('y'), la proposición resulta ser falsa.
Este punto es casi idéntico al Ejercicio 4 de la Práctica N° 4 de la guía (actualizada para el 1er cuatrimestre del 2007).

Punto V

(1)

Se debe demostrar que la relación es reflexiva, antisimétrica y transitiva.

Reflexividad

<tex>(x;y)R(x;y) \Leftrightarrow (x-y)^2 = (x-y)^2</tex>, y se cumple la reflexividad

Antisimetría

<tex>(x;y)R(w;z) \Leftrightarrow (x-y)^2 = (w-z)^2</tex>,y por conmutatividad de la igualdad se cumple que <tex>(w;z)R(x:y)</tex>

Transitividad

<tex>(a;b)R(c;d) \, \wedge \, (c;d)R(e;f) \, \Rightarrow \, (a-b)^2=(c-d)^2 \, \wedge \, (c-d)^2=(e-f)^2 \, \Rightarrow \\ \Rightarrow \, (a-b)^2=(e-f)^2 \, \Rightarrow \, (a;b)R(e;f)</tex>

(2)

<tex>cl[(1,2)] = \{ x \in R^2 / xR(1,2) \} = \{ x \in R^2 / (x_1 - x_2)^2 = (1-2)^2 = 1 \} </tex>
Dado este conjunto, se tiene que <tex>|x_1 - x_2| = 1</tex>. Entonces,
<tex> x_1 - x_2 = 1 \, \vee x_1 - x_2 = -1 \, \Rightarrow \\\Rightarrow \, x_2 = x_1 - 1 \, \vee x_2 = x_1 + 1 </tex>

Y el gráfico de dicho conjunto es

Para la siguiente clase pedida:
<tex>cl[(-1,2)]=\{ x \in R^2 / (x_1-x_2)^2=3^2=9 \} \, \Rightarrow \\\Rightarrow \, |x_1 - x_2| = 3 \, \Rightarrow \\\Rightarrow \, x_2 = x_1 - 3 \, \vee \, x_2 = x_1 + 3</tex>

Y el gráfico pedido es

Para la clase <tex>cl[(2,2)]</tex>:
<tex>cl[(2,2)] = \{x \in R^2 / (x_1-x_2)^2=0 \} \, \Rightarrow \\\Rightarrow \, x_1 = x_2 </tex>
Y el gráfico:

Y finalmente:
<tex>cl[(0,\sqrt{2})] = \{x \in R^2 / (x_1-x_2)^2 = \sqrt{2}^2 = 2 \} \, \Rightarrow \\\Rightarrow \, x_2 = x_1 - \sqrt{2} \, \vee \, x_2=x_1+\sqrt{2} </tex>
Y el gráfico sería:

(3)

El conjunto cociente sería <tex>R^2|_R = \{ [(0,x)] / x \in R_{\geq 0} \} </tex>
(con <tex>[(0,x)] = \{a \in R^2 / (a_1-a_2)^2=x^2 \} </tex>)
Considerar que para <tex>x=0</tex> se tiene la recta <tex>x_1=x_2</tex>, y a medida que se aumenta <tex>x</tex>, una recta para para arriba y la otra para abajo, barriendo todo <tex>R^2</tex>.
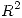Si se tratase con naturales, el conjunto cociente sería <tex>N^2|_R = \{[(0,x)] / x \in N_0 \} = \{ [(0,0)], [(0,1)], [(0,2)], ... \} </tex>

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.