12/12/12
MATEMÁTICA DISCRETA
Coloquio
- Definir isomorfismo para un par de álgebras de Boole.
- Demostrar que para todo
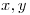 en
en 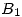 , si
, si  precede a
precede a  , entonces
, entonces 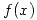 precede a
precede a 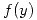 en
en 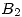 .
. - Sean
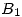 el álgebra de los divisores positivos de 154 y el álgebra de partes de
el álgebra de los divisores positivos de 154 y el álgebra de partes de 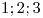 . Y el isomorfismo definido por:
. Y el isomorfismo definido por: 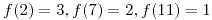
- Calcular
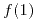 y
y 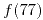 .
. - Dar los átomos de
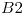 .
.
-
- Definir árbol.
- Demostrar que en un árbol
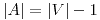 .
. - Probar que si
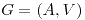 es árbol, el grafo
es árbol, el grafo 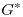 , que se construye a partir de
, que se construye a partir de 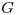 , quitando un vértice de grado 1 de
, quitando un vértice de grado 1 de 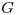 y la correspondiente arista, entonces
y la correspondiente arista, entonces 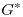 es árbol.
es árbol.
-
- Demostrar que si, en un grafo conexo simple, existen dos caminos de longitud máxima, entonces comparten al menos 1 vértice.
- ¿Vale la propiedad para grafos no conexos?
- Demostrar que un grafo es conexo si y sólo si existe su árbol generador mínimo.
- Demostrar que, siendo
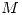 la matriz de adyacencia, el elemento
la matriz de adyacencia, el elemento 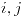 de la matriz
de la matriz 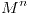 es igual a la cantidad de caminos de longitud
es igual a la cantidad de caminos de longitud  entre
entre 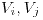 .
. - Demostrar que para un grafo simple de
 vértices, entonces al menos dos de ellos deben tener el mismo grado.
vértices, entonces al menos dos de ellos deben tener el mismo grado.
- Definir red de transporte, flujo en una red de transporte y su valore de corte en una red de transporte y su capacidad.
- Definir flujo maximal y corte minimal en una red de transporte.
- Probar que dados un flujo
 y un corte
y un corte  en una red de transporte, entonces:
en una red de transporte, entonces: 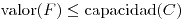
- ¿Qué puede decirse sobre
 y
y  si en el punto anterior se cumple la igualdad?
si en el punto anterior se cumple la igualdad?