27/07/11
MATEMÁTICA DISCRETA
Coloquio
- Sea R una relación de equivalencia en el conjunto A. Probar que
![<tex>\forall a,b \in A : a R b \leftrightarrow [a] = [b]</tex> <tex>\forall a,b \in A : a R b \leftrightarrow [a] = [b]</tex>](lib/plugins/latex/images/cd1d0e71205d44641533031e8485efa1302ab244_0.png) .
. - En
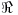 se define la relación
se define la relación 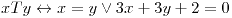 . Probar que es una relación de equivalencia. Hallar el conjunto cociente. ¿Existen clases con 3 elementos? ¿Y con 1 elemento?
. Probar que es una relación de equivalencia. Hallar el conjunto cociente. ¿Existen clases con 3 elementos? ¿Y con 1 elemento?
- Definir átomo de álgebra de Boole. Probar que el producto de dos átomos diferentes es 0.
- probar que la relación
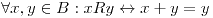 es de orden.
es de orden. - Probar que en un álgebra de Boole con el orden definido en (b) se cumple :
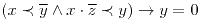 .
.
Faltan puntos…
Resolución
1.I
Por ser reflexiva R, se cumple que:
 por reflexión.
por reflexión.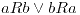 por simetría.
por simetría.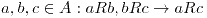 por transitividad.
por transitividad.
Tenemos que probar ![<tex>[a]=\{x\in A : xRa\}=\{x\in A : xRb\}=[b]</tex> <tex>[a]=\{x\in A : xRa\}=\{x\in A : xRb\}=[b]</tex>](lib/plugins/latex/images/c32447ef2783789e58b46e384e2e61ac0ba78626_0.png) .
.
Sea  un elemento cualquiera de [a] entonces
un elemento cualquiera de [a] entonces 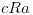 , y sabemos por hipotesis
, y sabemos por hipotesis 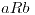 entonces por transitividad
entonces por transitividad 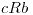 , por lo que
, por lo que ![<tex>c \in [b]</tex> <tex>c \in [b]</tex>](lib/plugins/latex/images/ed28060c594a6814641f5f4721a352734d887357_0.png) . Entonces cualquier elemento de [a] esta incluido en [b], por lo tanto podemos decir que [a]=[b].
. Entonces cualquier elemento de [a] esta incluido en [b], por lo tanto podemos decir que [a]=[b].
1.II
Para ser de equivalencia se debe cumplir que la relación cumpla reflexibidad, simetría y transitividad:
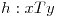
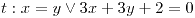
La implicación será verdadera si el valor de verdad de h es verdadero y además que el valor de verdad de alguno de los dos términos de t sea verdadero.
Reflexibidad:
Suponiendo h verdadero,  , entonces
, entonces  lo cual es verdadero. Entonces
lo cual es verdadero. Entonces 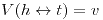 . T es reflexiva.
. T es reflexiva.
Simetría:
 Si
Si 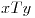 entonces se cumple que (
entonces se cumple que ( ó
ó 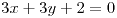 ). Por simetría de la igualdad y conmutación de la suma podemos decir que también se cumple (
). Por simetría de la igualdad y conmutación de la suma podemos decir que también se cumple (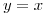 ó
ó 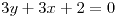 ) que sería la condición para que exista yTx . Por lo que
) que sería la condición para que exista yTx . Por lo que  es simétrica.
es simétrica.
Transitividad:
Si 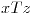 y
y 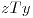 se cumple que (
se cumple que ( ó
ó 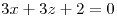 ) y que (
) y que (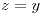 ó
ó 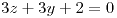 ).
).
si  y
y 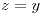 , entonces
, entonces  . Lo cual hace que exista
. Lo cual hace que exista 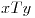 .
.
si  y
y 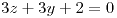 , entonces
, entonces 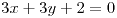 . Lo cual hace que exista
. Lo cual hace que exista 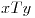 .
.
si 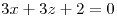 y
y 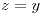 , entonces
, entonces 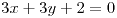 . Lo cual hace que exista
. Lo cual hace que exista 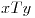 .
.
si 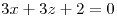 y
y 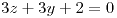 , restando ambas igualdades queda que
, restando ambas igualdades queda que  . Lo cual hace que exista
. Lo cual hace que exista 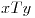 .
.
Entonces  es transitiva.
es transitiva.
Conjunto cociente:
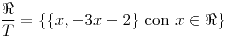
No existen clases con 3 elementos y existe una con 1 elemento cuando 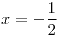 .
.