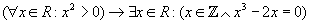20/12/06

MATEMÁTICA DISCRETA
Coloquio

  1. Dada la proposición
    1. Analizar el valor de verdad de la misma.
    2. Negar la proposición.
    3. Escribir las expresiones contraria, recíproca y contra-recíproca analizando en cada caso su valor de verdad.

    1. Definir ecuación de recurrencia lineal de orden n, ecuación caracteríastica o indicial y probar que: si 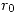<tex> \mathop{r_{0}} </tex> es solución de la ecuación indicial → 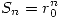<tex> \mathop{S_{n} = r_{0}^n} </tex> es solución de la ecuación de recurrencia.
    2. Resolver: <tex> \mathop{ a_{n} + n.a_{n-1} - 2.n.(n-1)a_{n-2} = 2.n! } </tex>.

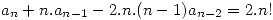  3. Sea 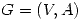<tex> \mathop{G = (V,A)} </tex> un grafo. Se dice que 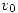<tex> \mathop{v_{0}} </tex> є V es un punto de articulación del grafo sii G' (el grafo que resulta de sacarle a G el vértice 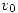<tex> \mathop{v_{0}} </tex> y todas las aristas incidentes en él) tiene más componentes conexas que G.
    1. Proporcione dos ejemplos de grafos con 6 vértices tal que uno tenga exactamente dos puntos de articulación y el otro ninguno.
    2. Probar que si G es un árbol 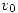<tex> \mathop{v_{0}} </tex> es un punto de articulación sii grado (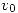<tex>\mathop{v_{0}} </tex>) > 1.

  4. Analizar el valor de verdad de las siguientes proposiciones justificando su respuesta
    1. Algunos grafos 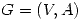<tex> \mathop{G = (V,A)} </tex> con <tex> \mathop{|A| = |V| -1 } </tex>no son árboles.
    2. Si G es un grafo conexo con por lo menos 2 vértices, uno de grado 1 y los demás de grado ≥ 2 entonces G es no acíclico.

    1. Definir red de transporte y flujo de una red.
    2. Probar que el valor del flujo saliente en el vértice fuente es igual al entrante en el sumidero.
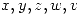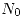    3. Hallar los valores de <tex> \mathop{x, y, z, w, v} </tex> є <tex> \mathop{N_{0}} </tex> para que constituyan un flujo compatible con la red dibujada.
    4. A partir del flujo de III que tenga el menor valor de x hallar el flujo máximo y corte minimal.