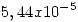Examen Parcial - 61.06. Probabilidad y Estadística A
 INDUSTIAL¿? No INDUSTRIAL¿?
INDUSTIAL¿? No INDUSTRIAL¿?
Cátedra: Baliña
Fecha: 1ºCuatrimestre 1º Oportunidad - 2006
Día: 15/05/2006
Enunciado
Punto I
Un equipo tiene dos componentes: A y B. El componente A se rompe, en promedio, cada 400hs; el componente B, cada 600hs. El equipo deja de funcionar cuando se rompe cualquiera de esos dos componentes.
¿Cuál es la probabilidad de que ese equipo funcione por menos de 800hs?
Punto II
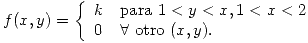
x: miles de unidades del producto A vendidas por mes; $2 cada una
y: miles de unidades del producto B vendidos por mes; $3 cada una
¿Cuál es la probabilidad de recaudar más de $7000 en un mes?
Punto III
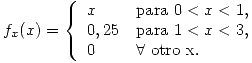
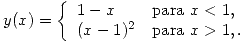
Calcular 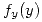
Punto IV
Unas galletitas tienen pedacitos de chocolate blanco y pedacitos de chocolate negro. Los pedacitos negros tienen una distribución de Poisson, con una media de 4 pedacitos/galleta; los blancos también tienen una distribución de Poisson pero la media es de 3 pedacitos/galleta. Un paquete de estas galletitas trae 8 unidades. ¿Cuál es la probabilidad de que en el mismo paquete haya al menos 2 galletitas sin ningún pedacito de chocolate?
Resolución
Punto I
Sea  la cantidad de tiempo que funciona la máquina A, con distribución exponencial negativa y
la cantidad de tiempo que funciona la máquina A, con distribución exponencial negativa y 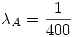 , y
, y 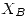 la cantidad de tiempo que funciona la máquina B, con distribución exponencial negativa y
la cantidad de tiempo que funciona la máquina B, con distribución exponencial negativa y 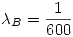 . De aquí en adelante, podemos resolver el problema de al menos dos maneras:
. De aquí en adelante, podemos resolver el problema de al menos dos maneras:
Opción 1:
La probabilidad de que el sistema dure menos de 800hs es 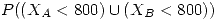 . Esto se debe a que el sistema trabaja “en serie”. Las dos situaciones NO son disjuntas, por lo que la unión debe expresarse como la suma de la probabilidad de cada una, menos la intersección (como son independientes, la intersección se calcula como el producto).
. Esto se debe a que el sistema trabaja “en serie”. Las dos situaciones NO son disjuntas, por lo que la unión debe expresarse como la suma de la probabilidad de cada una, menos la intersección (como son independientes, la intersección se calcula como el producto).
Opción 2
Como la duración del equipo viene dada por la del componente que se rompa primero, la distribución de su duración es la del mínimo entre 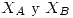 . La probabilidad de que se rompa antes de las 800hs sería integrar eso entre 0 y 800. Al buscar la fórmula para obtener la distribución del mínimo, tener en cuenta que son dos variables independientes con distinta tasa de falla.
. La probabilidad de que se rompa antes de las 800hs sería integrar eso entre 0 y 800. Al buscar la fórmula para obtener la distribución del mínimo, tener en cuenta que son dos variables independientes con distinta tasa de falla.
El resultado final es 0,9643.
Punto II
Primero se puede calcular el valor de k, sabiendo que la integral de 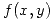 sobre todo el dominio tiene que ser igual a uno para que sea una función distribución de probabilidad. K resulta igual a 2.
sobre todo el dominio tiene que ser igual a uno para que sea una función distribución de probabilidad. K resulta igual a 2.
Luego, se realiza un cambio de variable a una 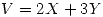 .
.
En base a 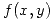 , se calcula
, se calcula 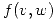 , que resulta ser
, que resulta ser  en
en 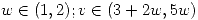 .
.
Se integra 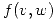 respecto de w para calcular la distribución marginal
respecto de w para calcular la distribución marginal 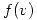 .
.
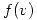 tiene dos ramas: una entre 5 y 7, y otra entre 7 y 10. Como piden la probabilidad de que gane MÁS de 7000, puede buscarse la distribución de una sola de las ramas y calcular:
tiene dos ramas: una entre 5 y 7, y otra entre 7 y 10. Como piden la probabilidad de que gane MÁS de 7000, puede buscarse la distribución de una sola de las ramas y calcular:
- La probabilidad de que gane menos de 7000 (integrando la rama entre 5 y 7) y restarla de 1.
- La probabilidad de que gane más de 7000 (integrando la rama entre 7 y 10).
Resultado: 0,6.
Punto III
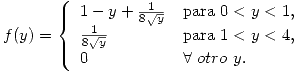
Punto IV
Se puede considerar un proceso Bernoulli el agarrar una galletita y comprobar si tiene algún copito o no.
La p de que no tenga copitos es la P de que no tenga blancos Y no tenga negros. Son independientes, así que esa intersección es el producto de ambas probabilidades . Otra opción es considerar una variable que represente el total de copitos (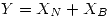 ); su distribución también será de Poisson y su media será la suma de las media
); su distribución también será de Poisson y su media será la suma de las media 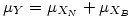 . En este caso,
. En este caso, 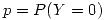 .
.
El número de veces que se lleva a cabo el experimento es 8 (n=8).
Como piden que AL MENOS 2 no tengan copitos, conviene sacar la P de que ninguna tenga copitos y la de que 1 no tenga copitos, sumarlas, y restarlas a 1.
Resultado: