Final - 61.06 Probabilidad y Estadística A (no industriales)
Cátedra: Todas
Fecha: 4° Oportunidad - (1º Cuatrimestre 2008)
Día: 30/07/2008
Punto 1
Sean a y b variables aleatorias independientes con distribución U[0,4]. Hallar la probabilidad de que 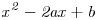 no tenga raíces reales.
no tenga raíces reales.
Punto 2
En un control de calidad de hormigón se extraen 3 probetas al azar. Cada una es probada para su resistencia a la compresión. Una probeta pasará la prueba si resiste por lo menos una carga axial de 5500kg. La resistencia a la rotura de las probetas puede ser modelada por una distribución normal de media 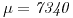 y desvío
y desvío 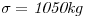 . La especificación requiere que las 3 probetas pasen la prueba para que el lote sea aceptado. El contratista prepara un lote cada día.
. La especificación requiere que las 3 probetas pasen la prueba para que el lote sea aceptado. El contratista prepara un lote cada día.
- a)¿Cuál es la probabilidad de que el primer lote rechazado sea el preparado el quinto día?
- b)El contratista puede mejorar la mezcla llevando la media de la distribución anterior a 8250kg. y reduciendo además el coeficiente de variación (σ / μ) en un 10% respecto del anterior. ¿Cuál sería entonces la probabilidad de que le sea rechazado por lo menos un lote en 10 días?
Punto 3
Lucas apuesta a que en 100 lanzamientos de una moneda honesta la cantidad de “caras” observadas diferirá de 50, en módulo, en 4 o más. ¿Cuál es la probabilidad de que Lucas pierda su apuesta? (Debe obtener un resultado numérico).
Punto 4
En una bodega se desea conocer la proporción p de barriles con el vino estacionado. En base a estudios previos, se le asigna a p la siguiente densidad: 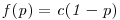 , si 0<p<1; 0 en otro caso. Un empleado prueba el vino de nueve barriles encontrando 5 barriles con el vino estacionado.
, si 0<p<1; 0 en otro caso. Un empleado prueba el vino de nueve barriles encontrando 5 barriles con el vino estacionado.
- a) Hallar la densidad a posteriori en base a los 9 resultados obtenidos.
- b) Estimar la proporción p.
Punto 5
Se tiene una población con distribución U(θ, θ+1). Basándose en una muestra de tamaño 1, 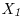 , diseñar una regla de decisión de nivel de significación 0.1, para verificar
, diseñar una regla de decisión de nivel de significación 0.1, para verificar 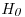 : θ ≤ 5 contra
: θ ≤ 5 contra 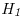 : θ >5. Grafique la curva característica operativa.
: θ >5. Grafique la curva característica operativa.
Resolución
Punto 1
Se presentan dos variables aleatorias independientes a y b con la misma distribución uniforme:
Como las variables son independientes, la función conjunta viene dada por: 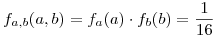
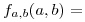
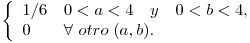
Se pide hallar la probabilidad de que 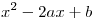 no tenga raíces reales, es decir que:
no tenga raíces reales, es decir que: 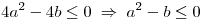
Planteo el cambio de variables:
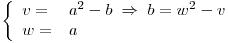
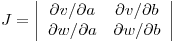

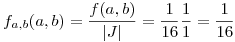
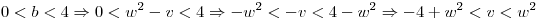
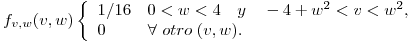
Procedo a marginar la función hallada para llegar a la expresión de 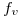 .
.
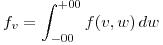
Si :
:
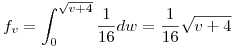
Si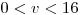 :
:
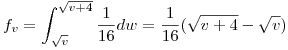

Como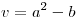 lo que me pide el problema es
lo que me pide el problema es
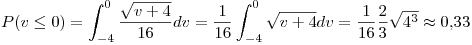
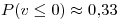 es el resultado pedido.
es el resultado pedido.
Punto 2
- Resistencia:
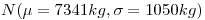
- Pasa la prueba si resiste 5500kg.
- Las tres probetas deben pasar la prueba para aceptar el lote.
- Hay un lote por día.
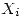 : resistencia de una probeta
: resistencia de una probeta
La probabilidad de que el lote apruebe es la probabilidad de que cada probeta pase la prueba, es decir:
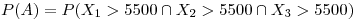
Como son sucesos independientes:
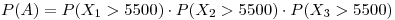
Como tienen la misma distribución:
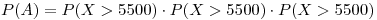
Por lo que 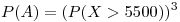

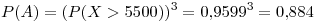
La probabilidad de aceptar un lote es 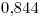 .
.
(a)Sabiendo que se preparara un lote por día, se plantea una variable geométrica de p = 1-0,884 = 0,116 donde el “éxito” es el rechazo de la muestra.
La probabilidad pedida es 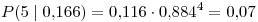
(b)
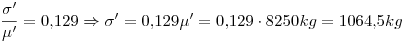
Por lo tanto 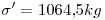
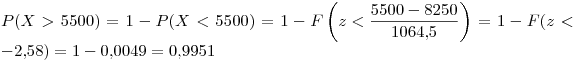

Ahora tenemos un proceso de Bernoulli de variable binomial con n = 10 y p = 1-0,9854 = 0,0146. Nos piden la probabilidad de que se rechace “por lo menos” un lote, es decir, un lote o más:

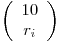
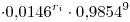
Punto 3
Se plantea una variable binomial con probabilidad de éxito en un ensayo p = 0,5. como se realizan 100 lanzamientos y además p = 0,5 el problema se puede resolver con una variable normal de media 
En el grafico están sombreadas los resultados que difieren de 50 en 4 o más caras.
La probabilidad de que Lucas pierda la apuesta es 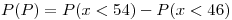
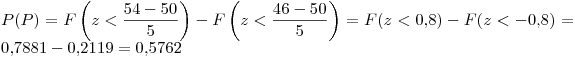
Por lo tanto, la probabilidad de que pierda es 
Punto 4
A priori se tiene 
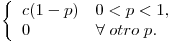
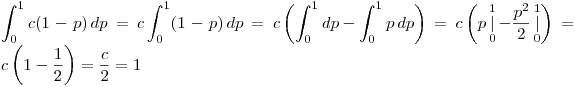
Por lo tanto  . Entonces nos queda:
. Entonces nos queda: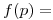

(a) La cantidad de vinos estacionados está dada por una variable binomial 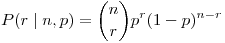
Esta es la probabilidad de los vinos estacionados dado p. El empleado probó el vino de nueve barriles encontrado 5 con vino estacionado:
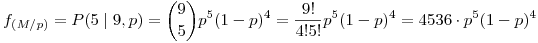
para 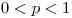
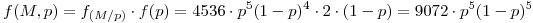
para 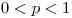
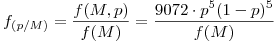
La función f(M) se puede obtener marginando f(M,p) de la siguiente manera:
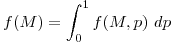
Como f(M,p) depende de la variable p únicamente, la integral será una constante.
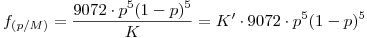
para 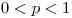
Siendo 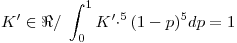
Por lo tanto, la densidad a posteriori de p en base a los nueve resultados obtenidos es:
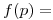
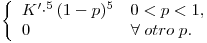
(b) La proporción p puede estimarse hallando la esperanza de su distribución: